Question

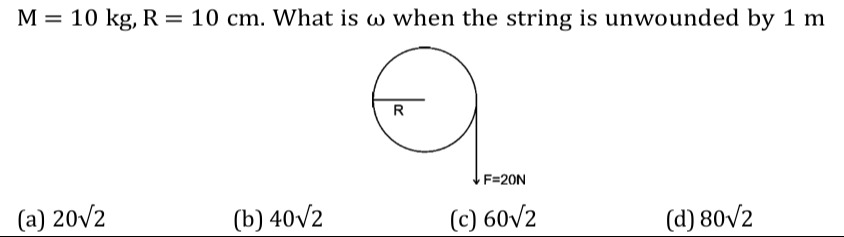
M = 10 kg, R = 10 cm. What is ω when the string is unwounded by 1 m

• A. 20√2
• B. 40√2
• C. 60√2
• D. 80√2

Answer 1

Answer: (A)

20√2 rad/s

Answer 2

Here's how to solve this problem:

1. Given:

   • Mass, $M = 10 \, \text{kg}$
   • Radius, $R = 10 \, \text{cm} = 0.1 \, \text{m}$
   • Force, $F = 20 \, \text{N}$
   • String unwound, $s = 1 \, \text{m}$

2. Determine the moment of inertia $I$ of the disk:

   $$I = \frac{1}{2} M R^2 = \frac{1}{2} \times 10 \times (0.1)^2 = 0.05 \, \text{kg} \cdot \text{m}^2$$

3. Relate linear displacement and angular displacement:

   $$s = R\theta \quad \Rightarrow \quad \theta = \frac{s}{R} = \frac{1}{0.1} = 10 \, \text{rad}$$

4. Calculate angular acceleration $\alpha$:

   • Torque, $\tau = F R = 20 \times 0.1 = 2 \, \text{N}\cdot \text{m}$
   • Then, $\alpha = \frac{\tau}{I} = \frac{2}{0.05} = 40 \, \text{rad/s}^2$

5. Use rotational kinematics (starting from rest):

   $$\omega^2 = \omega_0^2 + 2\alpha\theta \quad \text{with } \omega_0=0$$ $$\omega^2 = 2 \times 40 \times 10 = 800 \quad \Rightarrow \quad \omega = \sqrt{800} = 20\sqrt{2} \, \text{rad/s}$$