Question

Low spin complex of d5-cation in an octahedral field will have the following energy:
(A) $-2{{\Delta }_{0}}+P$
(B) $-2{{\Delta }_{0}}+2P$
(C) $\dfrac{-2}{5}{{\Delta }_{0}}+2P$
(D) $-2{{\Delta }_{0}}+3P$

Answer 1

The formula to give the Crystal Field Splitting Energy (CFSE) of a cation in an octahedral field is
$No.~of~electrons~in~\text{ }{{t}_{2g}}\times \left( -0.4 \right){{\Delta }_{0}}+no.~of~electrons~in~\text{ }{{e}_{g}}\times \left( 0.6 \right){{\Delta }_{0}}+electron\text{ }pairs\times pairing\text{ }energy(P)$
Try and apply this theory to the given scenario.

Complete step by step solution:
Let us first try and understand the Crystal Field Theory which governs the phenomenon required for us to give a correct answer in the given question.
The Crystal Field Theory (CFT) is a model for the bonding interaction between transition metals and ligands. It describes the effect of the attraction between the positive charge of the metal cation and negative charge on the non-bonding electrons of the ligand. When the ligands approach the central metal ion, the degeneracy of electronic orbital states, usually d or f orbitals, are broken due to the static electric field produced by a surrounding charge distribution.
The electrons in the d orbitals of the central metal ion and those in the ligand repel each other due to repulsion between like charges. Therefore, the d electrons closer to the ligands will have higher energy than those further away, which results in the d orbitals splitting in energy.
The d orbitals, as we know, can be divided into two smaller sets. The ${{d}_{{{x}^{2}}-{{y}^{2}}}}$ and ${{d}_{{{z}^{2}}}}$ orbitals point directly along the axes. On the other hand, the lobes of the ${{d}_{xy}}$, ${{d}_{yz}}$ and ${{d}_{zx}}$ orbitals lie between any two axes which are very evident from their symbols. When a ligand approaches these degenerate orbitals, this orientation of atomic orbitals splits them into two sets. The ${{e}_{g}}$ set comprises of ${{d}_{{{x}^{2}}-{{y}^{2}}}}$ and ${{d}_{{{z}^{2}}}}$ orbitals while the ${{t}_{2g}}$ set includes ${{d}_{xy}}$, ${{d}_{yz}}$ and ${{d}_{zx}}$ orbitals. In the case of octahedral complexes, the crystal field splitting results into the ${{e}_{g}}$set to be higher in energy while ${{t}_{2g}}$ set is lower in energy. The total crystal field splitting energy is represented as ${{\Delta }_{o}}$ where “o” in the subscript stands for octahedral complexes. The ${{t}_{2g}}$ and ${{e}_{g}}$ sets are not evenly split from the base energy value, which is also known as the barycentre, of the atomic orbitals. The values and the splitting are clear in the diagram below:

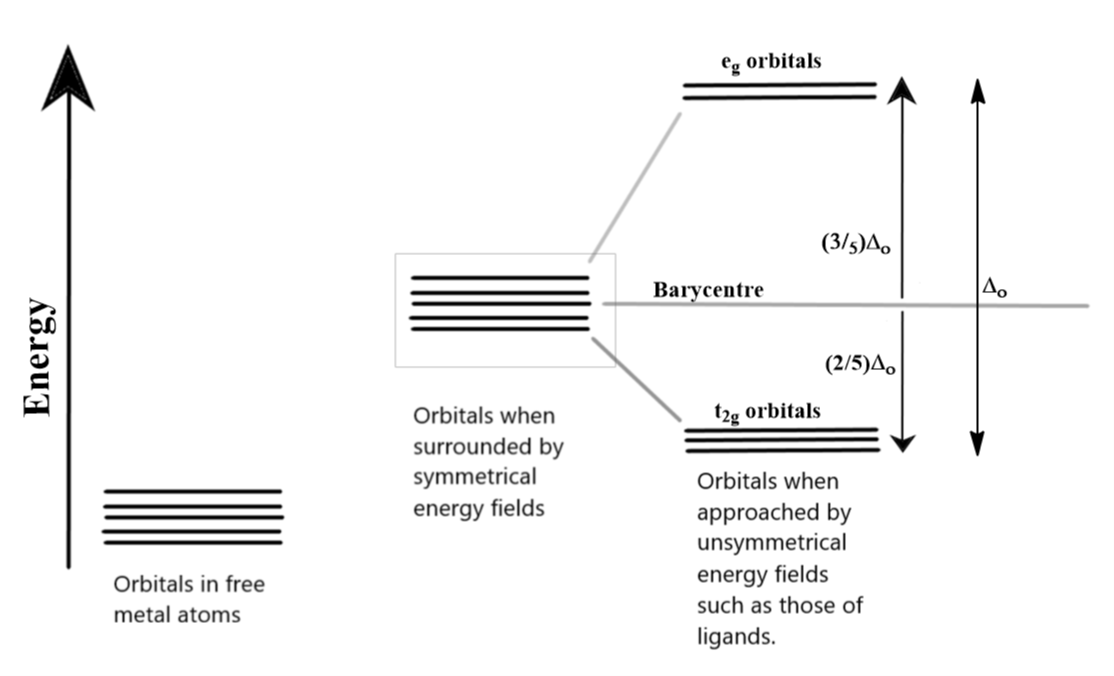
A low spin complex is formed when the next electron entering these split orbitals in the configuration of ${{d}^{4}}$ and onwards does not jump into the higher ${{e}_{g}}$ orbitals but pairs up with an existing electron in the lower${{t}_{2g}}$ orbitals. This happens only when the crystal field splitting energy (${{\Delta }_{o}}$) is higher than the pairing energy “P”. So the electronic configuration becomes ${{t}_{2g}}^{4}{{e}_{g}}^{0}$. This goes on until the configuration becomes ${{t}_{2g}}^{6}{{e}_{g}}^{0}$, after which the electrons start jumping up into higher energy d-orbitals because of the lack of space in the lower energy orbitals.
The configuration given here is ${{d}^{5}}$, so a low-spin complex would look like: ${{t}_{2g}}^{5}{{e}_{g}}^{0}$. Therefore, by the given formula, the Crystal Field Splitting Energy (CFSE) here is given by:

& 5\times \left( -0.4 \right){{\Delta }_{0}}+0\times \left( 0.6 \right){{\Delta }_{0}}+2\times pairing\text{ }energy(P) \\\ & \Rightarrow -2{{\Delta }_{0}}+2P \\\ \end{aligned}$$ **The answer to this question is option (B).** **Note:** Low spin complexes are only formed when the CFSE is higher than the pairing energy, in other words when the ligands attached to these orbitals have strong negative fields. Thus they are named as strong- field ligands. Some ligands produce weak fields and are termed as weak field ligands. In their case, the incoming electron in ${{d}^{4}}$ configuration moves to higher energy ${{e}_{g}}$ orbitals which make the electronic configuration as ${{t}_{2g}}^{3}{{e}_{g}}^{1}$. So lookout for the ligand and answer accordingly.