Solveeit Logo
Login

Question

Question: Let $f(x) = \frac{2x-3}{2025-(2\alpha^2-3\alpha)x}$. If $f(x)$ is Bijective in the following definit...

Let f(x)=2x−32025−(2α2−3α)xf(x) = \frac{2x-3}{2025-(2\alpha^2-3\alpha)x}. If f(x)f(x) is Bijective in the following definitions then find α\alpha?

  1. f:R−{20252α2−3α}→R−{2}f: R-\{\frac{2025}{2\alpha^2-3\alpha}\} \rightarrow R-\{2\}

  2. f:R→Rf: R \rightarrow R

Answer

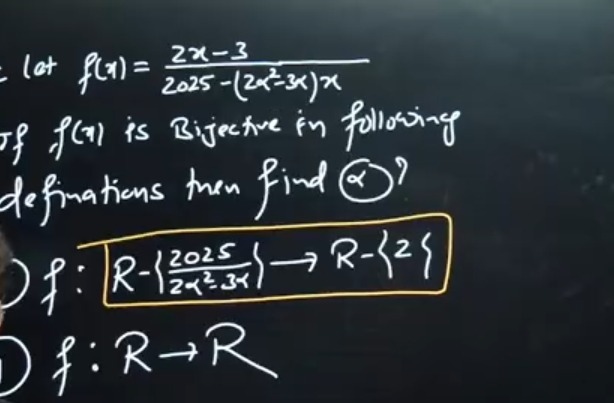
For definition 1, α∈{1,12}\alpha \in \{1, \frac{1}{2}\}. For definition 2, α∈{0,32}\alpha \in \{0, \frac{3}{2}\}.

Explanation

Solution

A rational function of the form f(x)=ax+bcx+df(x) = \frac{ax+b}{cx+d} is bijective if ad−bc≠0ad-bc \neq 0. If c≠0c \neq 0, the domain is R−{−dc}\mathbb{R} - \{-\frac{d}{c}\} and the range is R−{ac}\mathbb{R} - \{\frac{a}{c}\}.

Let K=2α2−3αK = 2\alpha^2-3\alpha. Then f(x)=2x−32025−Kxf(x) = \frac{2x-3}{2025-Kx}. Here a=2a=2, b=−3b=-3, c=−Kc=-K, d=2025d=2025. The injectivity condition is ad−bc=(2)(2025)−(−3)(−K)=4050−3K≠0ad-bc = (2)(2025) - (-3)(-K) = 4050 - 3K \neq 0.

Case 1: f:R−{20252α2−3α}→R−{2}f: R-\{\frac{2025}{2\alpha^2-3\alpha}\} \rightarrow R-\{2\} For the domain to be R−{2025K}R-\{\frac{2025}{K}\}, we must have K≠0K \neq 0. The range of a rational function is R−{ac}\mathbb{R} - \{\frac{a}{c}\}. In this case, the range is R−{2−K}\mathbb{R} - \{\frac{2}{-K}\}. For the function to be surjective onto R−{2}R-\{2\}, the range must be R−{2}R-\{2\}. Therefore, 2−K=2\frac{2}{-K} = 2, which implies −2=2K-2 = 2K, so K=−1K = -1. Substituting K=2α2−3αK = 2\alpha^2-3\alpha: 2α2−3α=−12\alpha^2-3\alpha = -1 2α2−3α+1=02\alpha^2-3\alpha+1 = 0 Factoring gives (2α−1)(α−1)=0(2\alpha-1)(\alpha-1) = 0. So, α=1\alpha = 1 or α=12\alpha = \frac{1}{2}. For these values, K=−1≠0K=-1 \neq 0, which is consistent with the domain definition. The injectivity condition 4050−3K=4050−3(−1)=4053≠04050 - 3K = 4050 - 3(-1) = 4053 \neq 0 is satisfied. Thus, for definition 1, α∈{1,12}\alpha \in \{1, \frac{1}{2}\}.

Case 2: f:R→Rf: R \rightarrow R For the domain to be RR, the denominator 2025−Kx2025-Kx must never be zero for any x∈Rx \in \mathbb{R}. This occurs if and only if the coefficient of xx is zero, i.e., K=0K=0. 2α2−3α=02\alpha^2-3\alpha = 0 Factoring gives α(2α−3)=0\alpha(2\alpha-3) = 0. So, α=0\alpha = 0 or α=32\alpha = \frac{3}{2}. If K=0K=0, the function becomes f(x)=2x−32025f(x) = \frac{2x-3}{2025}, which is a linear function with a non-zero slope. Linear functions with non-zero slopes are bijective from RR to RR. Thus, for definition 2, α∈{0,32}\alpha \in \{0, \frac{3}{2}\}.