Question

Look at the ray diagram shown, what will be the focal length of the ${1^{st}}$ and ${2^{nd}}$ lens, if the incident light ray passes without any deviation?

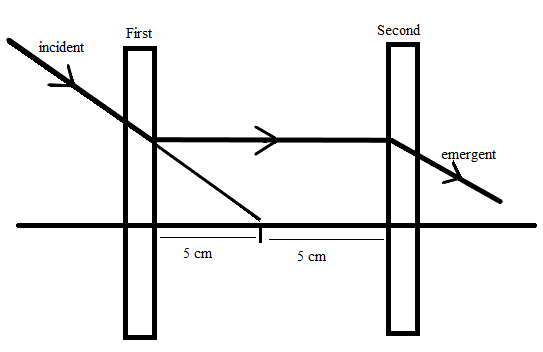
(A) $- 5cm, + 10cm$
(B) $+ 5cm, + 10cm$
(C) $- 5cm, + 5cm$
(D) $+ 5cm, - 5cm$

Answer 1

Hint : In this question, we need to determine the focal length of both the lenses such that incident light ray passes without any deviation. The solution can be approached by using the fact that a ray becomes parallel to the principal axis when it is passed through the focus of the lens. A ray parallel to the principal axis becomes convergent.

Complete Step By Step Answer:
Considering the first lens, it is clear from the diagram that the incident ray became parallel to the principal axis after passing through the lens. This means that the ray passed through its focus. Thus, focus of the first lens ${f_1}$ is $- 5cm$ .

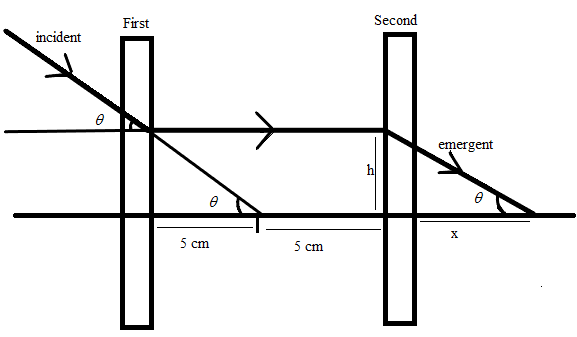
In the second lens, the ray which is incident parallel to the principal axis converged after passing through the lens which means that it passed through its focus. Consider the focal length of the second lens to be $x$ and the perpendicular distance between the ray parallel to the principal axis and the principal axis be $h$ as shown in the above figure.
Taking the tangent of the angle $\theta$ , we get
$\tan \theta = \dfrac{h}{5} = \dfrac{h}{x}$
$\Rightarrow x = 5cm$
$\Rightarrow {f_2} = x = 5cm$
$\therefore$ The correct option is C.

Additional Information:
A lens is a transparent object that is used to form an image of an object by incidenting rays of light from the object. It is usually circular in shape, both its surfaces polished, any one or both of its surfaces is curved and may be either convex or concave.

Note :
Lenses may be classified with respect to their two surfaces as biconvex, plano-convex and convexo-concave. Different rays of an incident light beam are refracted at different angles, so that all the parallel rays will converge or appear to diverge from a single point. This point is called the principal focus of the lens. The image formed by the lens may be real or virtual. Care should be taken in differentiating the converging and diverging lenses. There may be imperfections in the image of a point object known as aberrations.