Question
Question: Look at the diagram given in the figure which has been drawn with the ink of the uniform line of the...
Look at the diagram given in the figure which has been drawn with the ink of the uniform line of the thickness. The mass of the ink used to draw each of the two inner circles and each of the two line segments is m. The mass of the ink used to draw the outer circle is 6m. The coordinates of the center of the different parts are: outer circle (0, 0) left inner circle (-a, a), right inner circle (a, a), vertical line (0, 0) and horizontal line (0, a) the y – coordinates of the center of the mass of the ink in this drawing is:
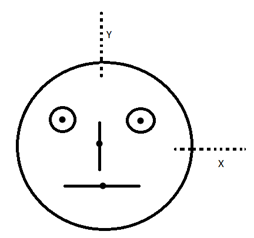
A. 10aB. 8aC. 12aD. 3a
Solution
In order to solve this question we have to use the formula of the center of the mass according to the y – axis which consists only y – coordinate of the system.
Formula used:
Ycom=M∑i=0nmiyi
Complete step by step solution:
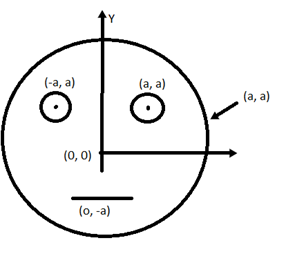
As we have to find center of the mass of y-axis we have to use the formula of the center of mass around y-axis:
Ycom=M∑i=0nmiyi
Where i = 0, 1, 2, 3…..
m = mass
Y is the coordinate of the y-axis
M is the total mass of the system.
Let us define all y coordinates and their masses of the given system:
Outer circle: -
Mass = 6m
y- Coordinate =0
Left inner circle:
Mass = m
y- Coordinate = a
Right inner circle:
Mass = m
y- Coordinate = a
Vertical line:
Mass = m
y- Coordinate = 0
Horizontal line:
Mass = m
y- Coordinate = -a
Now let’s substitute all the values in the formula.
⇒Ycm=6m+m+m+m+m(6m×0)+(m×a)+(m×a)+(m×0)+(m×−a)⇒Ycm=10m0+ma+ma+0-ma⇒Ycm=10mma∴Ycm=10a
Hence, the correct option is (A) 10a is correct.
Additional information:
Center of the mass: center of the mass of a body or the system of a particle is defined as a point at which whole of the mass of the body or all masses of a system of a particle appeared to be concentrated.
When we research the dynamics of the motion of a particle as a whole system,
We don’t need to think about the dynamics of the system’s individual particles.
But only concentrate on the dynamics of a particular point corresponding to that system.
Note:
When we are putting values of y- Coordinate we have to take extra concentration while putting positive and the negative signs of the coordinate if only a single coordinate is wrong it can change the whole answer.
