Question

$\log_x(x^2-1) \leq 0$

$x^2-1 > 0$

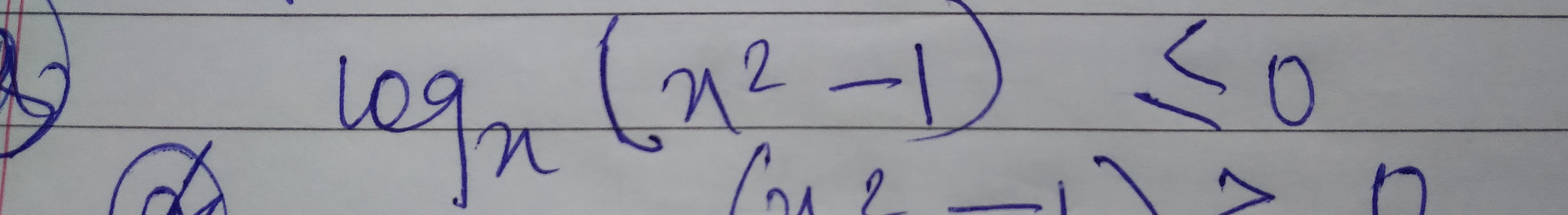
Answer 1

(1, $\sqrt{2}$]

Answer 2

To solve the inequality $\log_x(x^2-1) \leq 0$, we first establish the domain of the logarithmic function. The base $x$ must satisfy $x > 0$ and $x \neq 1$. The argument $x^2-1$ must be positive, so $x^2-1 > 0$, which implies $x^2 > 1$. This gives $x \in (-\infty, -1) \cup (1, \infty)$. Combining all these conditions, the valid domain for $x$ is $(1, \infty)$.

Since $x > 1$, the base of the logarithm is greater than 1, meaning the logarithmic function is strictly increasing. Therefore, $\log_x(x^2-1) \leq 0$ is equivalent to $x^2-1 \leq x^0$. $x^2-1 \leq 1$ $x^2-2 \leq 0$ Factoring the quadratic gives $(x-\sqrt{2})(x+\sqrt{2}) \leq 0$. This inequality holds for $x \in [-\sqrt{2}, \sqrt{2}]$.

Finally, we find the intersection of this solution with the established domain $(1, \infty)$. The intersection of $[-\sqrt{2}, \sqrt{2}]$ and $(1, \infty)$ is $(1, \sqrt{2}]$. The solution set is $1 < x \leq \sqrt{2}$.