Question
Question: $\log_x (125x) \cdot \log_{25}^{2} x = 1$ $\log_x 5^3x \cdot \log_{5^2}^{2} x = 1$ $\log_x 5^3x = \f...
logx(125x)⋅log252x=1 logx53x⋅log522x=1 logx53x=log522x1 logx53x=logx252 53x=
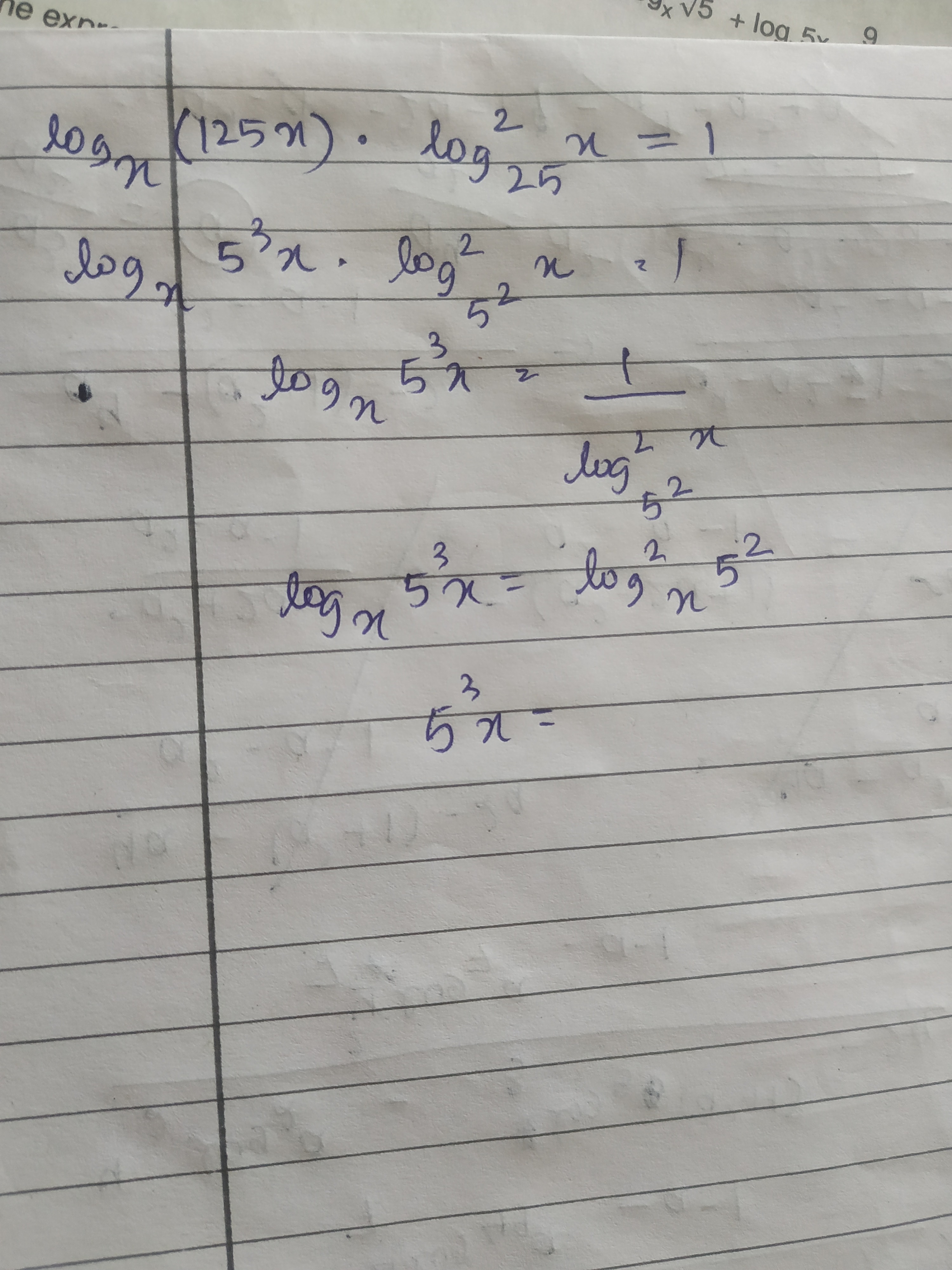
x=5,6251
Solution
Solution:
The given equation is logx(125x)⋅log252x=1.
First, we determine the domain for which the logarithms are defined. For logx(125x), we must have the base x>0 and x=1, and the argument 125x>0. Since 125>0, x>0. For log25x, we must have the base 25>0 and 25=1 (which are true), and the argument x>0. Combining these conditions, the domain is x>0 and x=1.
Now, we simplify the terms using logarithm properties, preferably converting to a common base, such as base 5. logx(125x)=log5xlog5(125x)=log5xlog5(53⋅x)=log5xlog553+log5x=log5x3+log5x. log25x=log525log5x=log552log5x=2log5x.
Substitute these expressions back into the original equation: (log5x3+log5x)⋅(2log5x)2=1.
Let y=log5x. Since x>0 and x=1, y can be any real number except log51=0. The equation becomes: (y3+y)⋅(2y)2=1. (y3+y)⋅4y2=1.
Since y=0, we can simplify the term yy2: 4(3+y)⋅y=1. Multiply both sides by 4: (3+y)y=4. 3y+y2=4. Rearrange the terms to form a quadratic equation: y2+3y−4=0.
We can solve this quadratic equation by factoring. We look for two numbers that multiply to -4 and add up to 3. These numbers are 4 and -1. (y+4)(y−1)=0.
This gives two possible values for y: y+4=0⟹y=−4. y−1=0⟹y=1.
Now, substitute back y=log5x to find the values of x.
Case 1: y=−4. log5x=−4. By the definition of logarithms, x=5−4. x=541=6251. This value of x is positive and not equal to 1, so it is a valid solution.
Case 2: y=1. log5x=1. By the definition of logarithms, x=51. x=5. This value of x is positive and not equal to 1, so it is a valid solution.
The solutions to the equation are x=5 and x=6251.
