Question
Question: Solve the logarithmic inequality $log_{\sqrt{8}}(x^2-4x+3)\leq 1$....
Solve the logarithmic inequality log8(x2−4x+3)≤1.
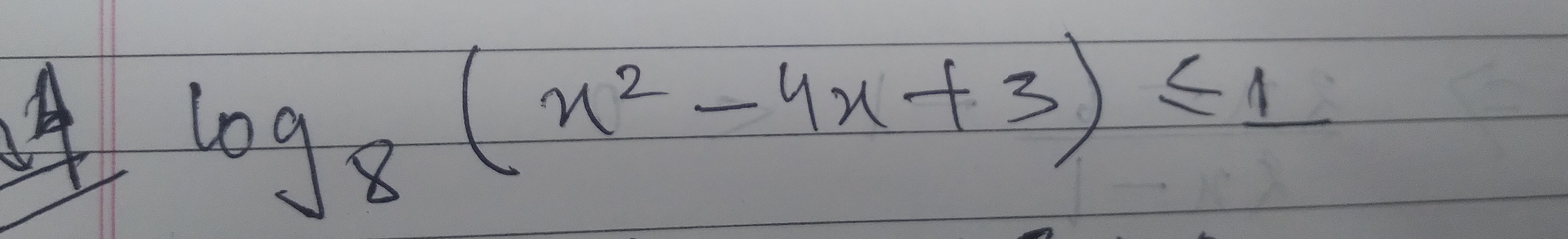
[2−1+22,1)∪(3,2+1+22]
(−∞,1)∪(3,∞)
[2−1+22,2+1+22]
(1,3)
[2−1+22,1)∪(3,2+1+22]
Solution
To solve the logarithmic inequality log8(x2−4x+3)≤1, we must satisfy two conditions:
-
Domain of the logarithm: The argument of the logarithm must be positive. x2−4x+3>0 (x−1)(x−3)>0 This inequality holds for x∈(−∞,1)∪(3,∞).
-
Solving the inequality: Since the base of the logarithm, 8, is greater than 1, we can remove the logarithm by raising the base to the power of the right side and maintaining the inequality direction. x2−4x+3≤(8)1 x2−4x+3≤8 x2−4x+(3−22)≤0
To find the roots of the quadratic equation x2−4x+(3−22)=0, we use the quadratic formula: x=24±(−4)2−4(1)(3−22) x=24±16−12+82 x=24±4+82 x=24±21+22 x=2±1+22
Let α=2−1+22 and β=2+1+22. The inequality x2−4x+(3−22)≤0 holds for x∈[α,β].
-
Intersection of conditions: We need to find the intersection of the domain (−∞,1)∪(3,∞) and the solution interval [2−1+22,2+1+22]. We note that 2−1+22<1 and 2+1+22>3. Therefore, the intersection is [2−1+22,1)∪(3,2+1+22].
