Question

$\log_{\sqrt{3}}(x+1)-\log_{3}(x-1) > \log_{4}4$

Answer 1

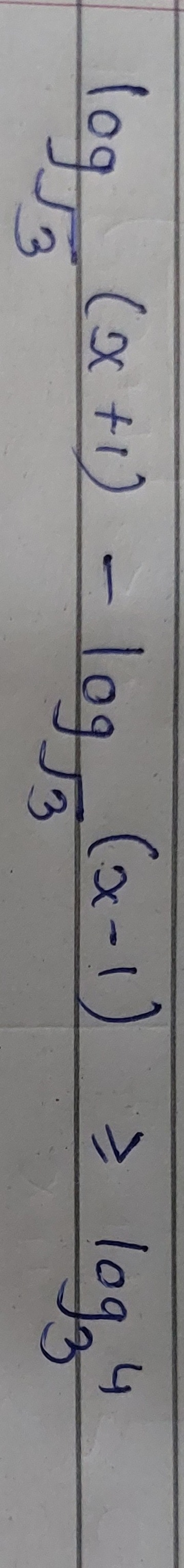
The solution to the inequality is $x > 1$. In interval notation, this is $(1, \infty)$.

Answer 2

Explanation of the solution:

1. Determine the domain of the inequality: For the logarithms $\log_{\sqrt{3}}(x+1)$ and $\log_{3}(x-1)$ to be defined, their arguments must be positive. Thus, $x+1 > 0$ and $x-1 > 0$. This implies $x > -1$ and $x > 1$. The intersection of these conditions gives the domain $x > 1$.

2. Simplify the inequality: The given inequality is $\log_{\sqrt{3}}(x+1)-\log_{3}(x-1) > \log_{4}4$.

   • Simplify the right side: $\log_{4}4 = 1$.
   • Convert the base of the first logarithm to 3: $\log_{\sqrt{3}}(x+1) = \log_{3^{1/2}}(x+1) = \frac{1}{1/2}\log_{3}(x+1) = 2\log_{3}(x+1)$.
   • The inequality becomes $2\log_{3}(x+1)-\log_{3}(x-1) > 1$.

3. Combine the logarithm terms: Using the properties of logarithms, $2\log_{3}(x+1) = \log_{3}(x+1)^2$.

   • The inequality becomes $\log_{3}(x+1)^2 - \log_{3}(x-1) > 1$.
   • Using the property $\log_b A - \log_b B = \log_b(A/B)$, we get $\log_{3}\left(\frac{(x+1)^2}{x-1}\right) > 1$.

4. Remove the logarithm: Since the base of the logarithm is $3 > 1$, the logarithmic function is increasing. We can remove the logarithm by exponentiating both sides with base 3, preserving the inequality direction:

   • $\frac{(x+1)^2}{x-1} > 3^1$
   • $\frac{(x+1)^2}{x-1} > 3$.

5. Solve the rational inequality:

   • $\frac{(x+1)^2}{x-1} - 3 > 0$
   • $\frac{(x+1)^2 - 3(x-1)}{x-1} > 0$
   • $\frac{x^2 + 2x + 1 - 3x + 3}{x-1} > 0$
   • $\frac{x^2 - x + 4}{x-1} > 0$.

6. Analyze the numerator and denominator: The numerator is the quadratic $x^2 - x + 4$. Its discriminant is $\Delta = (-1)^2 - 4(1)(4) = 1 - 16 = -15$. Since $\Delta < 0$ and the leading coefficient ($1$) is positive, the quadratic $x^2 - x + 4$ is always positive for all real values of $x$.

   • Thus, the sign of the fraction $\frac{x^2 - x + 4}{x-1}$ is determined solely by the sign of the denominator $x-1$.
   • For the fraction to be greater than 0, we must have $x-1 > 0$, which means $x > 1$.

7. Combine with the domain: The solution obtained from the inequality is $x > 1$. The domain of the original inequality is also $x > 1$. The intersection of these two conditions is $x > 1$.