Question
Question: $\log_{\frac{x+6}{3}}\left(\log_2{\frac{x-1}{x+2}}\right)>0$...
log3x+6(log2x+2x−1)>0
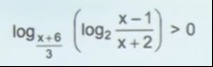
Answer
x \in (-6, -5) \cup (-3, -2)
Explanation
Solution
To solve the inequality log3x+6(log2x+2x−1)>0, we first determine the domain and then consider two cases based on the base of the logarithm.
1. Domain Determination:
- Argument of the inner logarithm: x+2x−1>0. This implies x∈(−∞,−2)∪(1,∞).
- Argument of the outer logarithm: log2x+2x−1>0. Since the base 2>1, this means x+2x−1>20=1. Solving x+2x−1>1 gives x+2−3>0, which implies x+2<0, so x<−2.
- Base of the outer logarithm: 3x+6>0 and 3x+6=1. This means x+6>0⟹x>−6, and x+6=3⟹x=−3.
Combining all conditions: x∈(−∞,−2), x>−6, and x=−3. The overall domain is x∈(−6,−3)∪(−3,−2).
2. Solving the Inequality: Let B=3x+6 and A=log2x+2x−1. The inequality is logB(A)>0.
-
Case 1: Base B>1 and Argument A>1.
- B>1⟹3x+6>1⟹x>−3. Within the domain, this is x∈(−3,−2).
- A>1⟹log2x+2x−1>1⟹x+2x−1>2. Solving x+2x−1>2 gives x+2−x−5>0⟹x+2x+5<0, which means x∈(−5,−2).
- The intersection of x∈(−3,−2) and x∈(−5,−2) is x∈(−3,−2).
-
Case 2: 0< Base B<1 and 0< Argument A<1.
- 0<B<1⟹0<3x+6<1⟹−6<x<−3. Within the domain, this is x∈(−6,−3).
- 0<A<1. We know A>0 implies x<−2. We need to solve A<1: log2x+2x−1<1⟹x+2x−1<2. Solving x+2x−1<2 gives x+2−x−5<0⟹x+2x+5>0, which means x∈(−∞,−5)∪(−2,∞).
- The intersection of x∈(−6,−3) and (x∈(−∞,−5)∪(−2,∞)) is x∈(−6,−5).
3. Combining Solutions: The total solution set is the union of the solutions from Case 1 and Case 2: x∈(−3,−2)∪(−6,−5). Therefore, the solution is x∈(−6,−5)∪(−3,−2).
