Question

$\log_8(x^2-4x+3) \le 1$

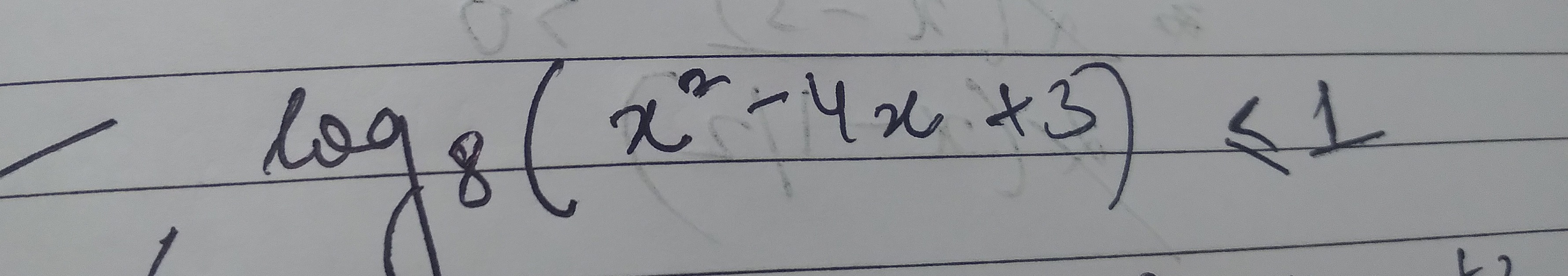
• A. [-1, 1) U (3, 5]
• B. (-inf, -1] U [5, inf)
• C. [-1, 5]
• D. (-inf, 1) U (3, inf)

Answer 1

Answer: (A)

[-1, 1) U (3, 5]

Answer 2

1. Domain: The argument of the logarithm must be positive: $x^2-4x+3 > 0$. Factoring yields $(x-1)(x-3) > 0$. This inequality holds for $x \in (-\infty, 1) \cup (3, \infty)$.
2. Inequality: Since the base of the logarithm $8 > 1$, we can exponentiate both sides while preserving the inequality direction: $x^2-4x+3 \le 8^1$ $x^2-4x+3 \le 8$ $x^2-4x-5 \le 0$ Factoring the quadratic gives $(x-5)(x+1) \le 0$. This inequality holds for $x \in [-1, 5]$.
3. Intersection: The solution must satisfy both the domain and the inequality. We find the intersection of $x \in (-\infty, 1) \cup (3, \infty)$ and $x \in [-1, 5]$. The intersection of $(-\infty, 1)$ with $[-1, 5]$ is $[-1, 1)$. The intersection of $(3, \infty)$ with $[-1, 5]$ is $(3, 5]$. Combining these, the solution is $x \in [-1, 1) \cup (3, 5]$.