Question

$\log_5{(3-2x)} \ge \log_5{(4x+1)}$

Answer 1

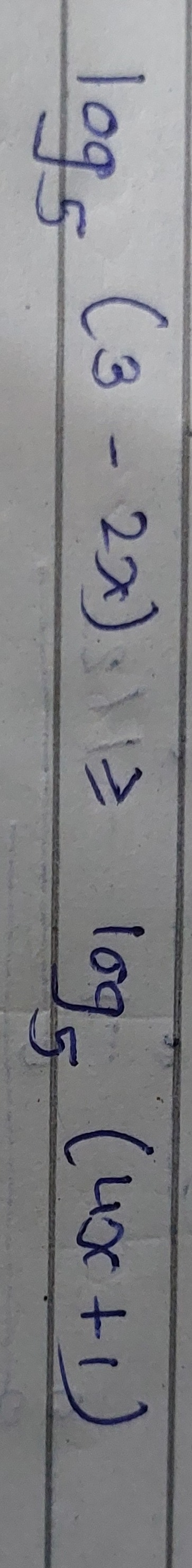
The solution set is $(-\frac{1}{4}, \frac{1}{3}]$.

Answer 2

We are asked to solve the inequality $\log_5{(3-2x)} \ge \log_5{(4x+1)}$.

For the logarithms to be defined, the arguments must be positive.

1. $3 - 2x > 0$

$3 > 2x$

$x < \frac{3}{2}$

2. $4x + 1 > 0$

$4x > -1$

$x > -\frac{1}{4}$

Combining these two conditions, the domain of the inequality is $-\frac{1}{4} < x < \frac{3}{2}$.

Since the base of the logarithm is $5$, which is greater than $1$, the inequality holds for the arguments in the same direction as the logarithms.

$\log_5{(3-2x)} \ge \log_5{(4x+1)} \implies 3 - 2x \ge 4x + 1$

Now, we solve this linear inequality:

$3 - 1 \ge 4x + 2x$

$2 \ge 6x$

$\frac{2}{6} \ge x$

$\frac{1}{3} \ge x$

$x \le \frac{1}{3}$

The solution to the original inequality must satisfy both the domain condition ($-\frac{1}{4} < x < \frac{3}{2}$) and the condition derived from comparing the arguments ($x \le \frac{1}{3}$). We need to find the intersection of the interval $(-\frac{1}{4}, \frac{3}{2})$ and the interval $(-\infty, \frac{1}{3}]$.

The intersection is $(-\frac{1}{4}, \frac{3}{2}) \cap (-\infty, \frac{1}{3}]$.

We need $x > -\frac{1}{4}$ and $x < \frac{3}{2}$ and $x \le \frac{1}{3}$.

Comparing the upper bounds, $\frac{1}{3} = \frac{2}{6}$ and $\frac{3}{2} = \frac{9}{6}$. Since $\frac{1}{3} < \frac{3}{2}$, the condition $x < \frac{3}{2}$ is automatically satisfied if $x \le \frac{1}{3}$.

Therefore, the intersection is $-\frac{1}{4} < x \le \frac{1}{3}$.

The solution set is the interval $(-\frac{1}{4}, \frac{1}{3}]$.

Explanation:

1. Determine the domain by requiring the arguments of the logarithms to be positive: $3-2x > 0 \implies x < 3/2$ and $4x+1 > 0 \implies x > -1/4$. The domain is $(-1/4, 3/2)$.
2. Since the base of the logarithm (5) is greater than 1, the inequality $\log_b a \ge \log_b c$ is equivalent to $a \ge c$. Apply this to the given inequality: $3-2x \ge 4x+1$.
3. Solve the resulting linear inequality: $3-2x \ge 4x+1 \implies 2 \ge 6x \implies x \le 1/3$.
4. The solution to the original inequality is the intersection of the domain and the solution from step 3: $(-1/4, 3/2) \cap (-\infty, 1/3] = (-1/4, 1/3]$.