Question

Solve the following inequality:

$\log_{4}(2x^{2}+3x+1) \le \log_{2}(2x+2)$

Answer 1

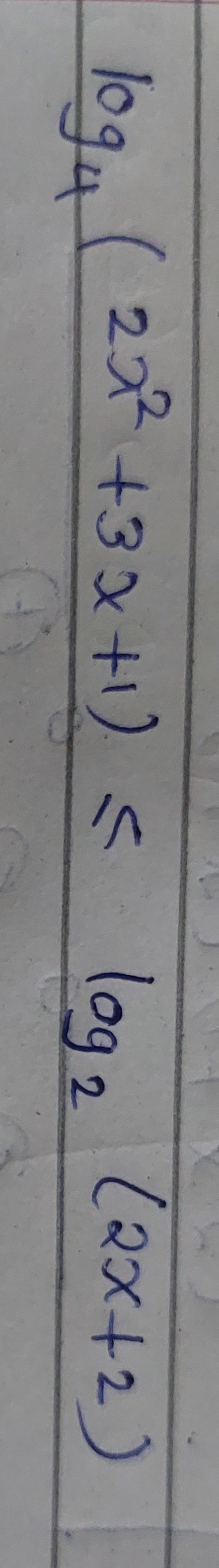
The solution set for the inequality is $x \in (-\frac{1}{2}, \infty)$.

Answer 2

1. Determine the domain by ensuring the arguments of the logarithms are positive: $2x^2+3x+1 > 0$ and $2x+2 > 0$. This yields the domain $x > -1/2$.

2. Rewrite the inequality using a common base (base 2): $\frac{1}{2}\log_2(2x^2+3x+1) \le \log_2(2x+2)$.

3. Simplify the inequality using logarithm properties: $\log_2(2x^2+3x+1) \le \log_2((2x+2)^2)$.

4. Remove the logarithms (since the base is > 1, the inequality direction is preserved): $2x^2+3x+1 \le (2x+2)^2$.

5. Solve the resulting quadratic inequality: $2x^2+3x+1 \le 4x^2+8x+4 \implies 2x^2+5x+3 \ge 0$. Factoring gives $(2x+3)(x+1) \ge 0$, which is true for $x \le -3/2$ or $x \ge -1$.

6. Find the intersection of the domain ($x > -1/2$) and the solution to the quadratic inequality ($x \le -3/2$ or $x \ge -1$). The intersection is $x > -1/2$.

Therefore, the solution set for the inequality is $x \in (-\frac{1}{2}, \infty)$.