Question

$\log_34 \lt \log_3(x-1)-\log_3(x+1)$

Answer 1

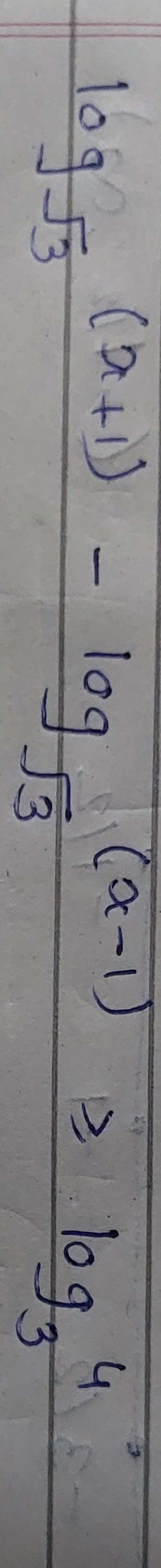
No solution

Answer 2

The given inequality is $\log_34 \lt \log_3(x-1)-\log_3(x+1)$.

1. Determine the domain of the inequality: For the logarithms to be defined, the arguments must be positive.

   $x-1 > 0 \implies x > 1$ $x+1 > 0 \implies x > -1$

   Both conditions must hold, so the domain is $x > 1$.

2. Simplify the inequality: Use the logarithm property $\log_b A - \log_b B = \log_b(A/B)$.

   $\log_34 \lt \log_3\left(\frac{x-1}{x+1}\right)$

3. Remove the logarithm: The base of the logarithm is 3, which is greater than 1. Since the logarithmic function with base 3 is increasing, we can remove the logarithm while preserving the inequality direction.

   $4 \lt \frac{x-1}{x+1}$

4. Solve the resulting inequality: Rearrange the inequality to solve for $x$.

   $\frac{x-1}{x+1} > 4$ $\frac{x-1}{x+1} - 4 > 0$ $\frac{(x-1) - 4(x+1)}{x+1} > 0$ $\frac{x-1 - 4x - 4}{x+1} > 0$ $\frac{-3x - 5}{x+1} > 0$

   Multiply both sides by -1 and reverse the inequality sign:

   $\frac{3x + 5}{x+1} < 0$

   To solve the rational inequality $\frac{3x + 5}{x+1} < 0$, find the critical points where the numerator or denominator is zero: $3x+5=0 \implies x = -5/3$ and $x+1=0 \implies x = -1$.

   Analyze the sign of $\frac{3x+5}{x+1}$ in the intervals determined by the critical points: $(-\infty, -5/3)$, $(-5/3, -1)$, and $(-1, \infty)$.

   • For $x < -5/3$, $\frac{(-)}{(-)} = (+)$.
   • For $-5/3 < x < -1$, $\frac{(+)}{(-)} = (-)$.
   • For $x > -1$, $\frac{(+)}{(+)} = (+)$.

   The inequality $\frac{3x + 5}{x+1} < 0$ is satisfied when $-5/3 < x < -1$.

5. Combine with the domain: The solution obtained from solving the inequality is $x \in (-5/3, -1)$. The domain of the original logarithmic inequality is $x \in (1, \infty)$.

   The solution set of the original inequality is the intersection of the solution from step 4 and the domain from step 1.

   Solution set = $(-5/3, -1) \cap (1, \infty)$.

   The interval $(-5/3, -1)$ is approximately $(-1.67, -1)$. The interval $(1, \infty)$ starts at 1 and extends to infinity. There is no overlap between these two intervals.

   The intersection is the empty set, $\emptyset$.