Question

$\log_2(x^2-5x+6)>1$

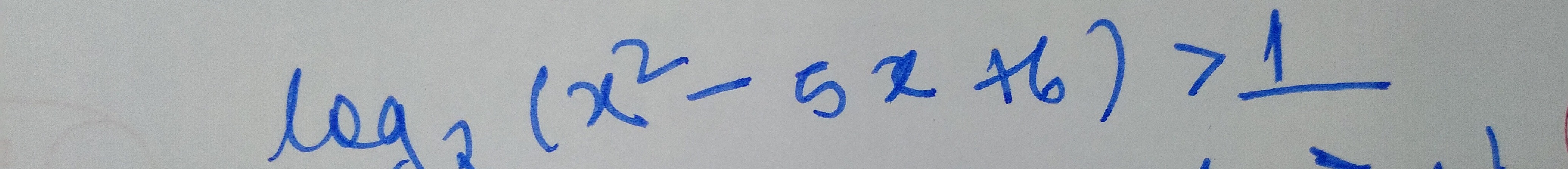
Answer 1

$x \in (-\infty, 1) \cup (4, \infty)$

Answer 2

1. Domain: $x^2-5x+6 > 0 \implies (x-2)(x-3) > 0 \implies x \in (-\infty, 2) \cup (3, \infty)$.
2. Inequality: $x^2-5x+6 > 2^1 \implies x^2-5x+4 > 0 \implies (x-1)(x-4) > 0 \implies x \in (-\infty, 1) \cup (4, \infty)$.
3. Intersection: The solution is the intersection of the domain and the inequality's solution, which is $x \in (-\infty, 1) \cup (4, \infty)$.