Question
Question: $\log_{18}(x^2-4x+3)<1$...
log18(x2−4x+3)<1
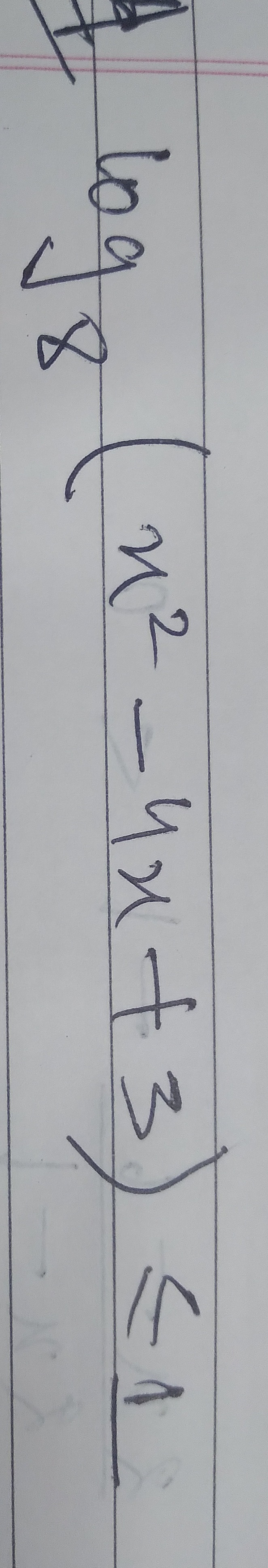
(2−19,1)∪(3,2+19)
x∈(−∞,1)∪(3,∞)
x∈(2−19,2+19)
(1,3)
(2−19,1)∪(3,2+19)
Solution
To solve the logarithmic inequality log18(x2−4x+3)<1, we must consider two conditions:
-
Domain of the logarithm: The argument of the logarithm must be strictly positive. x2−4x+3>0 Factoring the quadratic, we get: (x−1)(x−3)>0 This inequality holds when both factors are positive or both are negative.
- If x−1>0 and x−3>0, then x>1 and x>3, which means x>3.
- If x−1<0 and x−3<0, then x<1 and x<3, which means x<1. So, the domain is x∈(−∞,1)∪(3,∞).
-
Solving the inequality: The base of the logarithm is 18, which is greater than 1. Therefore, when we remove the logarithm, the direction of the inequality remains the same. x2−4x+3<181 x2−4x+3<18 Subtract 18 from both sides to get a standard quadratic inequality: x2−4x−15<0 To find the roots of the quadratic equation x2−4x−15=0, we use the quadratic formula x=2a−b±b2−4ac: x=2(1)−(−4)±(−4)2−4(1)(−15) x=24±16+60 x=24±76 x=24±4×19 x=24±219 x=2±19 Since the quadratic x2−4x−15 has a positive leading coefficient, its parabola opens upwards. Thus, the inequality x2−4x−15<0 holds for values of x between its roots: x∈(2−19,2+19).
-
Intersection of conditions: We must find the values of x that satisfy both the domain condition and the inequality condition. Domain: (−∞,1)∪(3,∞) Solution interval: (2−19,2+19) We need to approximate the values of the roots to determine the intersection. 16=4 and 25=5, so 19 is between 4 and 5. Approximately, 19≈4.36. 2−19≈2−4.36=−2.36 2+19≈2+4.36=6.36 So, the solution interval is approximately (−2.36,6.36). Now we find the intersection: ((−∞,1)∪(3,∞))∩(2−19,2+19) This intersection can be broken down as: (−∞,1)∩(2−19,2+19) which is (2−19,1) because 2−19<1. AND (3,∞)∩(2−19,2+19) which is (3,2+19) because 3<2+19. Combining these two parts, the final solution is (2−19,1)∪(3,2+19).
