Question

$\log_{10}(\log_23) + \log_{10}(\log_34) + \log_{10}(\log_45) + ....... + \log_{10}(\log_{1023}1024)$ simplifies to

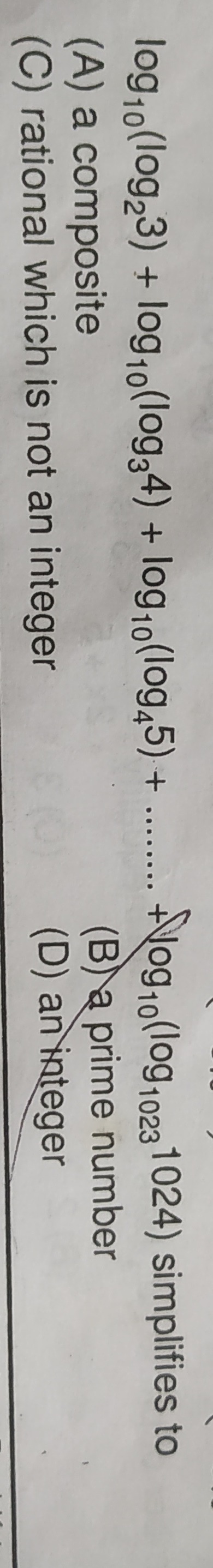
• A. a composite
• B. a prime number
• C. rational which is not an integer
• D. an integer

Answer 1

Answer: (D)

(D)

Answer 2

The given expression is:

$S = \log_{10}(\log_23) + \log_{10}(\log_34) + \log_{10}(\log_45) + ....... + \log_{10}(\log_{1023}1024)$

This is a sum of logarithms with base 10. Using the property $\log_b x + \log_b y = \log_b (xy)$, we can combine the terms into a single logarithm of a product:

$S = \log_{10} [ (\log_23) \times (\log_34) \times (\log_45) \times ....... \times (\log_{1023}1024) ]$

Let's evaluate the product inside the logarithm. The product is:

$P = (\log_23) \times (\log_34) \times (\log_45) \times ....... \times (\log_{1023}1024)$

We can use the change of base formula for logarithms: $\log_b a = \frac{\log_c a}{\log_c b}$. Let's use base 10 for the change of base, as it matches the outer logarithm's base:

$\log_23 = \frac{\log_{10}3}{\log_{10}2}$

$\log_34 = \frac{\log_{10}4}{\log_{10}3}$

$\log_45 = \frac{\log_{10}5}{\log_{10}4}$

...

$\log_{1023}1024 = \frac{\log_{10}1024}{\log_{10}1023}$

Substitute these expressions back into the product $P$:

$P = \left(\frac{\log_{10}3}{\log_{10}2}\right) \times \left(\frac{\log_{10}4}{\log_{10}3}\right) \times \left(\frac{\log_{10}5}{\log_{10}4}\right) \times ....... \times \left(\frac{\log_{10}1024}{\log_{10}1023}\right)$

This is a telescoping product. The numerator of each term cancels with the denominator of the next term:

$P = \frac{\cancel{\log_{10}3}}{\log_{10}2} \times \frac{\cancel{\log_{10}4}}{\cancel{\log_{10}3}} \times \frac{\cancel{\log_{10}5}}{\cancel{\log_{10}4}} \times ....... \times \frac{\log_{10}1024}{\cancel{\log_{10}1023}}$

The product simplifies to:

$P = \frac{\log_{10}1024}{\log_{10}2}$

Using the change of base formula in reverse ($\frac{\log_c a}{\log_c b} = \log_b a$), we get:

$P = \log_2 1024$

Now, we need to evaluate $\log_2 1024$. We need to find the power to which 2 must be raised to get 1024.

$2^{10} = 1024$

So, $\log_2 1024 = 10$.

The value of the product $P$ is 10.

Now, substitute this value back into the expression for $S$:

$S = \log_{10} [ P ] = \log_{10} [ 10 ]$

The logarithm of a number to the same base is 1:

$\log_{10} 10 = 1$

The simplified value of the expression is 1.

Therefore, the answer is an integer.