Question

Locus of the centres of the circles, which touch the circle ${{x}^{2}}+{{y}^{2}}=1$ externally and also touch the y-axis and lie in the first quadrant is
[a] $y=\sqrt{1+4x},x\ge 0$
[b] $x=\sqrt{1+4y},y\ge 0$
[c] $x=\sqrt{1+2y},y\ge 0$
[d] $y=\sqrt{1+2x},x\ge 0$

Answer 1

Assume that the centre of the circle is (h,k) and the radius is r. Use the fact that the circle touches the y-axis and hence y-axis is tangent to it and hence find the value of r in terms of h and k. Use the fact that if two circles touch each other externally, then the distance between their centres is equal to the sum of the radii of the two circles. Hence forma an equation in h and k. Replace h by x and k by y to get locus of the point. Note that as the circle lies in the first quadrant h > 0 and k > 0.

Complete step-by-step answer:

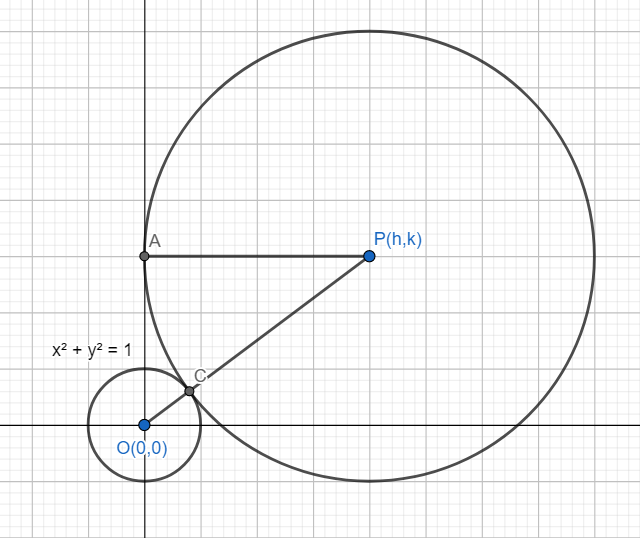
Let P(h,k) be the coordinates of the centre of the circle touching the circle ${{x}^{2}}+{{y}^{2}}=1$and the y-axis and lying in the first quadrant and let r be its radius.
Since the circle touches the y-axis, y-axis is tangent of the circle and hence PA is perpendicular to y-axis. Also, PA is equal to the radius of the circle. Since PA is perpendicular to y-axis, we have PA = h (The abscissa of the point P).
Hence, we have r = h.
Also, since the circle touches the circle ${{x}^{2}}+{{y}^{2}}=1$, we have the distance PO is equal to the sum of the radii of the two circles.
Radius of ${{x}^{2}}+{{y}^{2}}=1$ is $\sqrt{1}=1$ and the radius of the circle with centre (h,k) is h.
Also, we have by distance formula
$PO=\sqrt{{{h}^{2}}+{{k}^{2}}}$
Hence, we have
$\sqrt{{{h}^{2}}+{{k}^{2}}}=1+h$
Squaring both sides, we get
$\begin{aligned} & {{h}^{2}}+{{k}^{2}}={{h}^{2}}+1+2h \\\ & \Rightarrow {{k}^{2}}=2h+1 \\\ & \Rightarrow k=\pm \sqrt{2h+1} \\\ \end{aligned}$
Since the circle lies in the first quadrant, we have $k\ge 0$ and hence, we have
$k=\sqrt{2h+1},h\ge 0$
Replace h by x and k by y, we get
$y=\sqrt{2x+1},x\ge 0$
So, the correct answer is “Option d”.

Note: Alternative solution:
Consider the line x = -1 as shown in the diagram

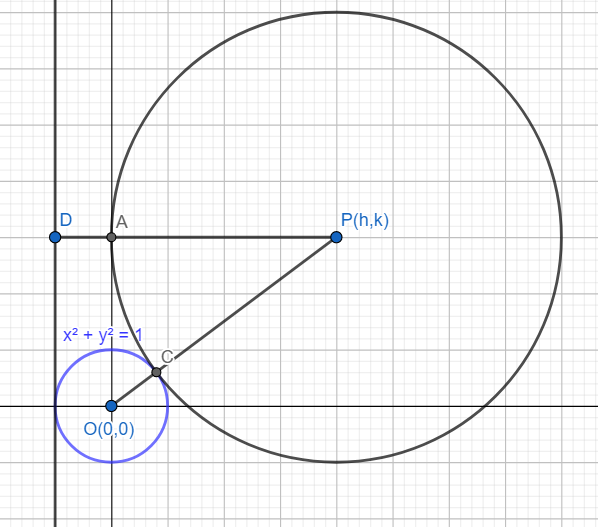
Observe that PD = PA +AD = r+1 and PO = PC + CO= r+1
Hence, we have PD = PO
Hence locus of point P is a parabola with directrix x = -1 and focus (0,0)
Hence, the equation of locus of point P is
${{y}^{2}}=4a\left( x+k \right)$
Where a and k need to be determined.
Since vertex is the midpoint of the point where the axis meets the directrix and focus, we have
Coordinates of vertex are $\left( \dfrac{0-1}{2},\dfrac{0+0}{2} \right)=\left( \dfrac{-1}{2},0 \right)$
Hence, we have
$k=\dfrac{1}{2}$
Since a is the distance of vertex from the directrix, we have $a=\dfrac{1}{2}$
Hence, we have
${{y}^{2}}=2\left( x+\dfrac{1}{2} \right)=2x+1$
Since $y\ge 0$, we have
$y=\sqrt{2x+1}$, which is the same as obtained above.
Hence option [d] is correct.