Question

Locus of points from which perpendicular tangents can be drawn to the circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$ is
(a) A circle passing through origin
(b) A circle of radius $2a$
(c) Concentric circle of radius $a\sqrt{2}$
(d) None of these.

Answer 1

For solving this problem we assume that the point from which the tangents are drawn as $\left( h,k \right)$ and we take the equation of tangent as general form of equation that is $y=mx+c$ where $'m'$ is a slope of tangent and $'c'$ is some constant. By substituting the line equation we get a value of $'c'$. By substituting the point in line equation we get a value of $'c'$. By equating both the values of $'c'$ we get the quadratic equation in $'m'$ since the tangents are perpendicular by taking the product of slopes as ‘-1’ we get the required locus.

Complete step-by-step solution

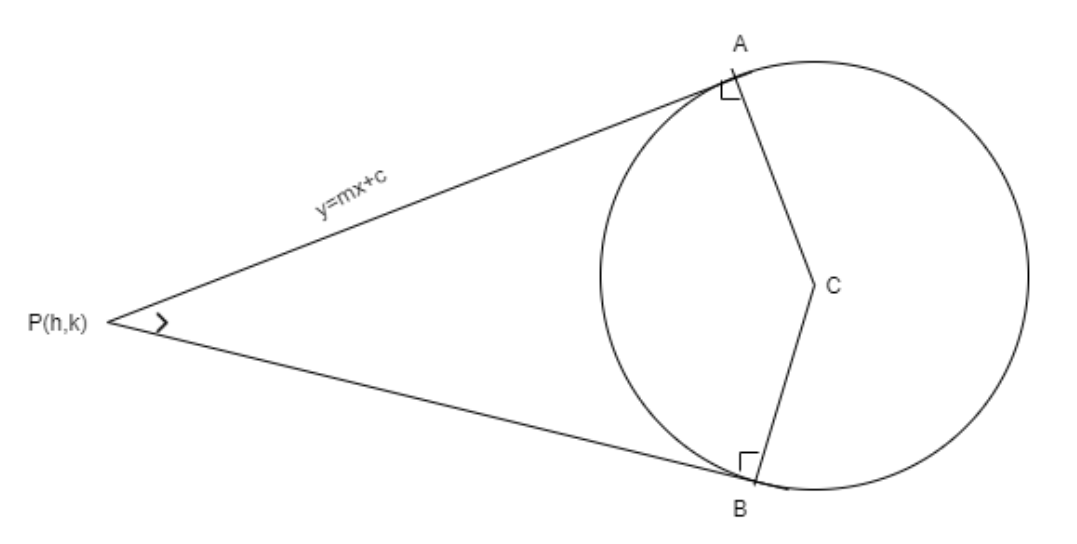
Let us assume that the point from where the tangents are drawn as $P\left( h,k \right)$
Let us assume that the equation of tangent as $y=mx+c$ where $'m'$ is the slope of the tangent and $'c'$ is some constant.
Here, we know that the tangent is passing through $P\left( h,k \right)$.
So, $P\left( h,k \right)$ satisfies the tangent equation. By substituting $P\left( h,k \right)$ in tangent equation we get

& \Rightarrow y=mx+c \\\ & \Rightarrow k=mh+c \\\ & \Rightarrow c=mh-k......equation(i) \\\ \end{aligned}$$ We know that the tangent and the circle will intersect. So, let us substitute the value of $$y=mx+c$$ in circle equation given as $${{x}^{2}}+{{y}^{2}}={{a}^{2}}$$ we get $$\begin{aligned} & \Rightarrow {{x}^{2}}+{{\left( mx+c \right)}^{2}}={{a}^{2}} \\\ & \Rightarrow {{x}^{2}}+{{m}^{2}}{{x}^{2}}+2mxc+{{c}^{2}}={{a}^{2}} \\\ & \Rightarrow {{x}^{2}}\left( 1+{{m}^{2}} \right)+x\left( 2mc \right)+\left( {{c}^{2}}-{{a}^{2}} \right)=0 \\\ \end{aligned}$$ Since, we know that the tangent touches the circle, the discriminant of the above equation should be zero. The discriminant of quadratic equation $$a{{x}^{2}}+bx+c=0$$ is given as $${{b}^{2}}-4ac$$. By comparing the above equation with general equation of quadratic equation we get $$\begin{aligned} & \Rightarrow {{\left( 2mc \right)}^{2}}-4\left( {{c}^{2}}-{{a}^{2}} \right)\left( 1+{{m}^{2}} \right)=0 \\\ & \Rightarrow 4{{m}^{2}}{{c}^{2}}-4{{c}^{2}}\left( 1+{{m}^{2}} \right)+4{{a}^{2}}\left( 1+{{m}^{2}} \right)=0 \\\ & \Rightarrow {{c}^{2}}\left( -1 \right)+{{a}^{2}}\left( 1+{{m}^{2}} \right)=0 \\\ & \Rightarrow {{c}^{2}}={{a}^{2}}\left( 1+{{m}^{2}} \right)....equation(ii) \\\ \end{aligned}$$ By substituting the value of $$'c'$$ we got from equation (i) in equation (ii) we get $$\begin{aligned} & \Rightarrow {{\left( mh-k \right)}^{2}}={{a}^{2}}\left( 1+{{m}^{2}} \right) \\\ & \Rightarrow {{m}^{2}}{{h}^{2}}-2mhk+{{k}^{2}}={{a}^{2}}+{{a}^{2}}{{m}^{2}} \\\ & \Rightarrow {{m}^{2}}\left( {{h}^{2}}-{{a}^{2}} \right)-2mhk+\left( {{k}^{2}}-{{a}^{2}} \right)=0....equation(iii) \\\ \end{aligned}$$ We know that from the above equation we get two values of $$'m'$$ which gives two equations of tangents. We are given that the tangents are perpendicular so the product of two slopes is ‘-1’. For the general quadratic equation $$a{{x}^{2}}+bx+c=0$$ the product of roots is given as$$\dfrac{c}{a}$$. By applying the product of roots to equation (iii) we get $$\begin{aligned} & \Rightarrow \dfrac{{{k}^{2}}-{{a}^{2}}}{{{h}^{2}}-{{a}^{2}}}=-1 \\\ & \Rightarrow {{k}^{2}}-{{a}^{2}}=-{{h}^{2}}+{{a}^{2}} \\\ & \Rightarrow {{h}^{2}}+{{k}^{2}}={{\left( a\sqrt{2} \right)}^{2}} \\\ \end{aligned}$$ By replacing $$\left( h,k \right)$$ by $$\left( x,y \right)$$ we get locus of point $$P\left( h,k \right)$$ as $$\Rightarrow {{x}^{2}}+{{y}^{2}}={{\left( a\sqrt{2} \right)}^{2}}$$ Therefore, the required locus is a circle with radius $$a\sqrt{2}$$. **So, option (c) is the correct answer.** **Note:** This problem can be solved in other methods also. We know that the equation of tangent to general equation of circle $${{x}^{2}}+{{y}^{2}}={{a}^{2}}$$ is given as $$y=mx\pm a\sqrt{1+{{m}^{2}}}$$. We also know that point $$P\left( h,k \right)$$ lies on the tangent we can write $$\begin{aligned} & \Rightarrow k=mh\pm a\sqrt{1+{{m}^{2}}} \\\ & \Rightarrow k-mh=\pm a\sqrt{1+{{m}^{2}}} \\\ \end{aligned}$$ By squaring on both sides we get $$\begin{aligned} & \Rightarrow {{\left( mh-k \right)}^{2}}={{a}^{2}}\left( 1+{{m}^{2}} \right) \\\ & \Rightarrow {{m}^{2}}{{h}^{2}}-2mhk+{{k}^{2}}={{a}^{2}}+{{a}^{2}}{{m}^{2}} \\\ & \Rightarrow {{m}^{2}}\left( {{h}^{2}}-{{a}^{2}} \right)-2mhk+\left( {{k}^{2}}-{{a}^{2}} \right)=0....equation(iii) \\\ \end{aligned}$$ We know that from the above equation we get two values of $$'m'$$ which gives two equations of tangents. We are given that the tangents are perpendicular so the product of two slopes is ‘-1’. For the general quadratic equation $$a{{x}^{2}}+bx+c=0$$ the product of roots is given as$$\dfrac{c}{a}$$. By applying the product of roots to equation (iii) we get $$\begin{aligned} & \Rightarrow \dfrac{{{k}^{2}}-{{a}^{2}}}{{{h}^{2}}-{{a}^{2}}}=-1 \\\ & \Rightarrow {{k}^{2}}-{{a}^{2}}=-{{h}^{2}}+{{a}^{2}} \\\ & \Rightarrow {{h}^{2}}+{{k}^{2}}={{\left( a\sqrt{2} \right)}^{2}} \\\ \end{aligned}$$ By replacing $$\left( h,k \right)$$ by $$\left( x,y \right)$$ we get locus of point $$P\left( h,k \right)$$ as $$\Rightarrow {{x}^{2}}+{{y}^{2}}={{\left( a\sqrt{2} \right)}^{2}}$$ Therefore, the required locus is a circle with radius $$a\sqrt{2}$$. So, option (c) is the correct answer.