Question

Locate the points representing the complex numbers $z$ for which $\left| z \right|<1$ .

Answer 1

Hint: For solving this problem first we should know the geometrical meaning of $\left| z \right|=r$ where $z$ is any complex number and $r$ is any positive number. Then, we will give the correct answer to this question very easily.

Complete step-by-step answer:
Given: We have to locate the points representing the complex numbers $z$ for which $\left| z \right|<1$ .
Now, before we proceed to locate the point we should know what is the geometrical meaning of $\left| z \right|=r$ where $z$ is any complex number and $r$ is any positive number.
Now, let $z=x+iy$ is a complex number where $x$ and $y$ are real numbers.
Now, the modulus value of $z$ is defined as $\left| z \right|=\sqrt{{{x}^{2}}+{{y}^{2}}}$ .
Now, let $\left| z \right|=r$ . Then,
$\begin{aligned} & \left| z \right|=\sqrt{{{x}^{2}}+{{y}^{2}}}=r \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}={{r}^{2}} \\\ \end{aligned}$
Now, as we know that ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$ is the equation of a circle whose centre is at the origin (0,0) and radius of the circle is $r$ units. Then, $\left| z \right|=r$ also represents a circle of radius $r$ whose centre is at the origin (0,0).
Thus, we can say that $\left| z \right|<1$ and ${{x}^{2}}+{{y}^{2}}<1$ have the same geometrical meaning. And as we know that ${{x}^{2}}+{{y}^{2}}<1$ represents all the points inside the circle whose centre is at the origin and has radius 1 units. The plot of ${{x}^{2}}+{{y}^{2}}=1$ is shown in the figure below:

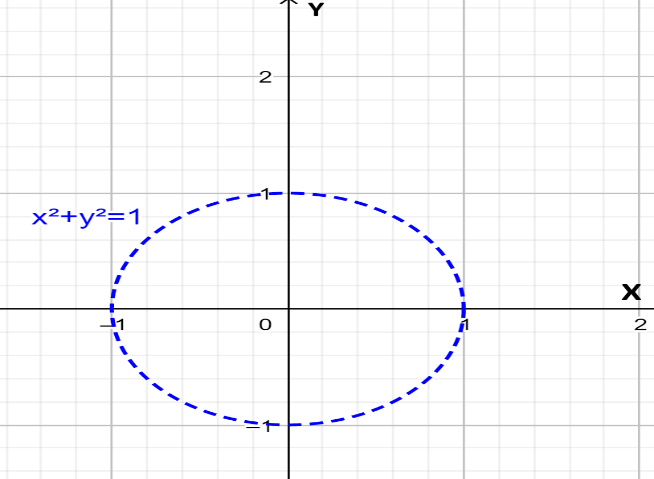
Now, we can say that $\left| z \right|<1$ represents all the points inside the circle shown in the above figure. Mathematically we can write it like for $z=x+iy$ such that x\in \left[ 0,1 \right]\sim \left\\{ 1 \right\\} and y\in \left[ 0,1 \right]\sim \left\\{ 1 \right\\} .

Note: Here, the concept of the geometrical meaning of modulus value of any complex number should be crystal clear to the student then apply the concept without any confusion to get the correct answer.