Question

$LO{{L}^{'}},MO{{M}^{'}}$ are two chords of a parabola passing through a point O on its axis. Prove that the radical axis of the circles described on $L{{L}^{'}},M{{M}^{'}}$ has diameter through the vertex of the parabola.

Answer 1

Hint: Suppose points $L,{{L}^{'}},M,{{M}^{'}}$ as parametric coordinates on the parabola ${{y}^{2}}=4ax$. General parametric coordinates on ${{y}^{2}}=4ax$is given as ${{y}^{2}}=4ax$. Find the equation of circles with the help of diametric form of equation of circle, given as
$\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)+\left( y-{{y}_{1}} \right)\left( y-{{y}_{2}} \right)=0$
Where, $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ are the extreme ends of the diameter. Radical axis of two conics is given by the equation ${{s}_{1}}-{{s}_{2}}=0$, where ${{s}_{1}},{{s}_{2}}$are the equation of curves.

Complete step-by-step answer:
Let us suppose the equation of parabola is ${{y}^{2}}=4ax$. And here, two chords $LO{{L}^{'}},MO{{M}^{'}}$ are drawn meeting at o on the axis of parabola and hence, we need to prove the radical axis of circles described on $L{{L}^{'}},M{{M}^{'}}$ as diameters passes through the vertex of the parabola.
Now, as ${{y}^{2}}=4ax$ is symmetric about the x-axis and vertex of it will lie at (o, o).
So, the diagram with the help of given information, is given as

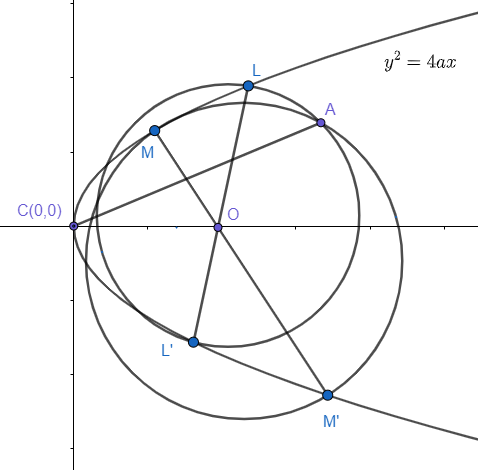
Where, AC is the radical axis of both the circles.$LO{{L}^{'}},MO{{M}^{'}}$ are chords for the parabola and acting as diameters for two circles.
Let us suppose the points $L,{{L}^{'}}\to L\left( a{{t}^{2}},2a{{t}_{1}} \right),{{L}^{'}}\left( a{{t}^{2}}_{2},2a{{t}_{2}} \right)$
And points.$M,{{M}^{'}}\to M\left( a{{t}^{2}}_{3},2a{{t}_{3}} \right),{{M}^{'}}\left( a{{t}^{2}}_{4},2a{{t}_{4}} \right)$
We know equation of line passing through two points $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ can be given as
$y-{{y}_{1}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\left( x-{{x}_{1}} \right)$ ………………….(i)
So, equation of $L{{L}^{'}}$given as

& y-2a{{t}_{2}}=\dfrac{2a{{t}_{2}}-2a{{t}_{1}}}{a{{t}_{2}}^{2}-a{{t}_{1}}^{2}}\left( x-a{{t}_{2}}^{2} \right) \\\ & y-2a{{t}_{2}}=\dfrac{2\left( {{t}_{2}}-{{t}_{1}} \right)}{{{t}_{2}}^{2}-{{t}_{1}}^{2}}\left( x-a{{t}_{2}}^{2} \right) \\\ & y-2a{{t}_{2}}=\dfrac{2\left( {{t}_{2}}-{{t}_{1}} \right)}{\left( {{t}_{2}}-{{t}_{1}} \right)\left( {{t}_{2}}+{{t}_{1}} \right)}\left( x-a{{t}_{2}}^{2} \right) \\\ & \dfrac{y-2a{{t}_{2}}}{1}=\dfrac{2\left( x-a{{t}_{2}}^{2} \right)}{\left( {{t}_{2}}+{{t}_{1}} \right)} \\\ & y\left( {{t}_{1}}+{{t}_{2}} \right)-2a{{t}_{2}}\left( {{t}_{2}}+{{t}_{1}} \right)=2\left( x-a{{t}_{2}}^{2} \right) \\\ & y\left( {{t}_{1}}+{{t}_{2}} \right)-2a{{t}_{2}}^{2}-2a{{t}_{1}}{{t}_{2}}=2x-2a{{t}_{2}}^{2} \\\ \end{aligned}$$ $$2x-\left( {{t}_{1}}+{{t}_{2}} \right)y+2a{{t}_{1}}{{t}_{2}}=0$$…………………(ii) Similarly, we can write the equation of $M{{M}^{'}}$ by using the equation (i) as well. So, we get the equation of $M{{M}^{'}}$, just similar to equation (ii), as $$2x-\left( {{t}_{3}}+{{t}_{4}} \right)y+2a{{t}_{3}}{{t}_{4}}=0$$………………..(iii) Now, we can get point o by putting y = 0 to the equations (ii) and (iii). So, putting y = 0 in equation (ii), we get $2x+2a{{t}_{1}}{{t}_{2}}=0$ $x=-a{{t}_{1}}{{t}_{2}}$…………(iv) And putting y = 0 in equation (iii), we get $$2x+2a{{t}_{3}}{{t}_{4}}=0$$ $$x=-a{{t}_{3}}{{t}_{4}}$$…………………..(v) Now, as o point is the intersection of $LO{{L}^{'}},MO{{M}^{'}}$. It means the expressions (iv) and (v) should be equal. So, we get $\begin{aligned} & -a{{t}_{1}}{{t}_{2}}=-a{{t}_{3}}{{t}_{4}} \\\ & a{{t}_{1}}{{t}_{2}}=a{{t}_{3}}{{t}_{4}} \\\ \end{aligned}$ Let us suppose above terms are equal to another constant C. So, we get $a{{t}_{1}}{{t}_{2}}=a{{t}_{3}}{{t}_{4}}=c$ ${{t}_{1}}{{t}_{2}}=\dfrac{c}{a},{{t}_{3}}{{t}_{4}}=\dfrac{c}{a}$…………….(vi) Now, we know equation of circle in diameter form is given as $\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)+\left( y-{{y}_{1}} \right)\left( y-{{y}_{2}} \right)=0$ ………………….(vii) Where $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ are the extreme points of the diameter. So, equation of circle through $L{{L}^{'}}$ as diameter, can be given as $\begin{aligned} & \left( x-a{{t}_{1}}^{2} \right)\left( x-a{{t}_{2}}^{2} \right)+\left( y-2a{{t}_{1}} \right)\left( y-2a{{t}_{2}} \right)=0 \\\ & {{x}^{2}}-a{{t}_{1}}^{2}x-a{{t}_{2}}^{2}x+{{a}^{2}}{{t}_{1}}^{2}{{t}_{2}}^{2}+{{y}^{2}}-2a{{t}_{1}}y \\\ & -2a{{t}_{2}}y+4{{a}^{2}}{{t}_{1}}{{t}_{2}}=0, \\\ & {{x}^{2}}+{{y}^{2}}-a\left( {{t}_{1}}^{2}+{{t}_{2}}^{2} \right)x-2a\left( {{t}_{1}}+{{t}_{2}} \right)y+{{a}^{2}}{{t}_{1}}^{2}{{t}_{2}}^{2}+4{{a}^{2}}{{t}_{1}}{{t}_{2}} \\\ \end{aligned}$ Now, we can replace ${{t}_{1}}{{t}_{2}}\to \dfrac{c}{a}$in the above equation, from equation (vi). So, we get ${{x}^{2}}+{{y}^{2}}-a\left( {{t}_{1}}^{2}+{{t}_{2}}^{2} \right)x-2a\left( {{t}_{1}}+{{t}_{2}} \right)y+{{a}^{2}}\times \dfrac{{{c}^{2}}}{{{a}^{2}}}+4{{a}^{2}}\dfrac{c}{a}=0$ ${{x}^{2}}+{{y}^{2}}-a\left( {{t}_{1}}^{2}+{{t}_{2}}^{2} \right)x-2a\left( {{t}_{1}}+{{t}_{2}} \right)y+{{c}^{2}}+4ac=0$…………..(viii) Now, similarly, we can write the equation of circle taking $M{{M}^{'}}$ as diameter. So, we get ${{x}^{2}}+{{y}^{2}}-a\left( {{t}_{3}}^{2}+{{t}_{4}}^{2} \right)x-2a\left( {{t}_{3}}+{{t}_{4}} \right)y+{{c}^{2}}+4ac=0$ ………………..(ix) Now, as we know radical axis for any two conics with the equations ${{s}_{1}},{{s}_{2}}$ can be given by relation ${{s}_{1}}-{{s}_{2}}=0$…………..(x) So, radical axis for both the circles represented in equation (viii) and (ix) is given as $\begin{aligned} & \left[ {{x}^{2}}+{{y}^{2}}-a\left( {{t}_{1}}^{2}+{{t}_{2}}^{2} \right)x-2a\left( {{t}_{1}}+{{t}_{2}} \right)y+{{c}^{2}}+4ac \right]-\left[ {{x}^{2}}+{{y}^{2}}-a\left( {{t}_{3}}^{2}+{{t}_{4}}^{2} \right)x-2a\left( {{t}_{3}}+{{t}_{4}} \right)y+{{c}^{2}}+4ac \right]=0 \\\ & x\left( {{t}_{3}}^{2}+{{t}_{4}}^{2}-{{t}_{1}}^{2}-{{t}_{2}}^{2} \right)+y\left[ 2a\left( {{t}_{3}}+{{t}_{4}} \right)-2a\left( {{t}_{1}}+{{t}_{2}} \right) \right]=0 \\\ \end{aligned}$ $x\left[ {{t}_{3}}^{2}+{{t}_{4}}^{2}-{{t}_{1}}^{2}-{{t}_{2}}^{2} \right]+2ay\left[ {{t}_{3}}+{{t}_{4}}-{{t}_{1}}-{{t}_{2}} \right]=0$………………(xi) Now, we can observe that the above equation is passing through (o, o) i.e. vertex of the parabola. It means the radical axis of both the given circles is passing through the vertex of the parabola. Hence, the given statement is proved. Note: Calculation is the important side of these kinds of questions and using parametric coordinates also help to solve these problems easily. One may suppose points of chords as $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right),\left( {{x}_{4}},{{y}_{4}} \right)$ as well. But it will make the solution longer and complex, as we need to use other four equations i.e. ${{y}_{1}}^{2}=4a{{x}_{1}},{{y}_{2}}^{2}=4a{{x}_{2}}$ and so on; it means using the parametric coordinates with these kind of problem is the key point of the question as well. Equation of radical axis and common chord of two circles are the same. So, don’t confuse the given equation ${{s}_{1}}-{{s}_{2}}=0$ as well. Be clear with the direct results in conic sections, it makes the solution easier and less time taking.