Question
Question: ln the adjacent diagram, CP represents a wavefront and AO and BP, the corresponding two rays. The co...
ln the adjacent diagram, CP represents a wavefront and AO and BP, the corresponding two rays. The condition on θ for constructive interference at P between the ray BP and reflected ray OP is:
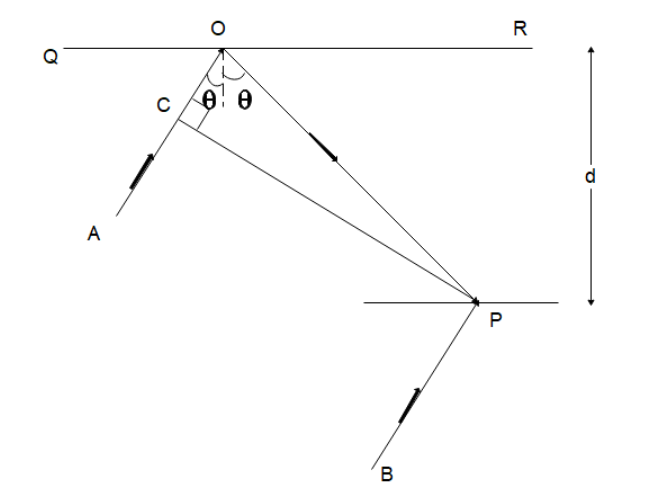
A) cosθ=2d3λ
B) cosθ=4dλ
C) secθ−cosθ=dλ
D) secθ−cosθ=d4λ
Solution
In this solution, we will first calculate the extra distance by the ray AO before it reaches the point P which will be the path difference of the two rays. There will be constructive interference if the path difference is an integral multiple of the wavelength of the two waves. However, in this case, the reflection of one of the rays from the top surface will flip the condition for constructive interference.
Complete step by step answer:
From the diagram, we can see that while the two rays AO and BP are parallel to each other the ray AO will have to travel an extra distance before it reaches the point P. We know that this is the path difference between the two rays. Let us find the extra distance the ray AO has to travel.
Since the line CP represents a wavefront, the extra distance, the ray AO will travel will be the sum of distance CO and OP.
We can find the distance BP from triangle OPM as:
cosθ=OPd
⇒OP=cosθd
For CO, we can see that
cos2θ=OPCO
As OP=cosθd, we can write
⇒CO=cosθdcos2θ
Now the net path difference will be
D=CO+OP
⇒D=cosθd(cos2θ+1)
Since cos(2θ+1)=2cos2θ, we have
D=2dcosθ
Under normal circumstances, the path difference would have to be equal to an integral multiple of wavelengths. But in this case, the reflection of the ray OP causes an additional path difference of λ/2. Hence the condition of the constructive interference, in this case, will be
⇒ D=2nλ which we can write as
⇒ 2dcosθ=2nλ
Which gives us
cosθ=4dnλ
For n=1,
cosθ=4dλ which corresponds to option (B).
Note: We must be careful to include the reflection of the ray OP and its effect on an additional path difference in the ray. For this, we have assumed that the medium outside OQ is rarer than the medium where the waves are propagating.
