Question

Lithium forms body-centered cubic structure. The length of the side of its unit cell is 351 pm. Atomic radius of lithium will be:
A. 75pm
B. 300pm
C. 240pm
D. 152pm

Answer 1

In a body centered unit length the radius and side length are related by the equation $r=(\surd 3\div 4)\times a$, where a is the edge length of the unit cell. Use this equation to derive the atomic radius of the element.

Complete step-by step solution:
In order to understand the question, let us first understand the structure of a body-centered cubic unit cell. The diagram is given below:

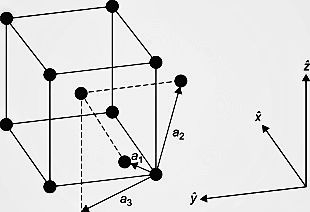
-As we can see from the figure, in BCC, there are 8 atoms at the 8 edges of the cube and one atom is present at the centre of the cube. All of these contribute to the BCC structure and let us find their individual contributions.
-As there are 8 edges in a cube and all of them are filled with 8 atoms, then we can say that each atom in the edge has a contribution of 1 8 to the BCC structure. There is a single atom present at the centre of the cube, so it is counted as 1 i.e full contribution to the cell.
-Hence, the total contribution of BCC cell is $$$$$$(1\times (1\div 8))from\text{ }edges+1\text{ }from\text{ }body\text{ }centre=\text{ }2\text{ }atoms$. -Also, the body diagonal has a length that is 4 times the radius of the atom,r. Using Pythagoras theorem, we get the relation as$r=(\surd 3\div 4)\times a$$
-Substituting the value of a as 351 pm, we have
$r=\dfrac{\sqrt{3}}{4} \times 351 pm = 152pm$

So we obtain the radius of the lithium atom as 152pm.,

Note: As the question does not contain SI units and the answer too, it is not at all required to change pico metre to metre. It will consume more time. Take √3 to be approximately 1.73. Also remember that the packing fraction of BCC is about 68%.