Question

Lines ${{L}_{1}}:\ y-x=0$ and ${{L}_{2}}:\ 2x+y=0$ intersect the line ${{L}_{3}}:\ y+2=0$ at P and Q respectively. The bisector of the acute angle between ${{L}_{1}}$and ${{L}_{2}}$intersects ${{L}_{3}}$ at R.
Statement-1: The ratio $PQ:RQ$ equals $2\sqrt{2}:\sqrt{5}$, because
Statement-2: In any triangle, the bisector of an angle divides the triangle into two similar triangles.
(a). Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
(b). Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.
(c). Statement 1 is true, statement 2 is false.
(d). Statement 1 is false, statement 2 is true.

Answer 1

Hint: First construct everything as said in the equation. All the lines will form a triangle. Find the points P, Q, R. Then find the distances PQ, RQ. So, you can see P, Q, R lie on a single line. You know the coordinates of all points P, Q. As we know OR is angle bisector. WE can say that the ratio of OP, OQ is the same as the ratio of PR, RQ. So, we can find OP, OQ by distance formula. IF there is distance d between points $\left( a,b \right)$ and $\left( c,d \right)$ the d is given by
$d\ =\ \sqrt{{{\left( a-c \right)}^{2}}+{{\left( b-d \right)}^{2}}}$

Complete step-by-step answer:

The lines ${{L}_{1}}:\ y-x=0$, ${{L}_{2}}:\ 2x+y=0$and ${{L}_{3}}:\ y+2=0$ are:

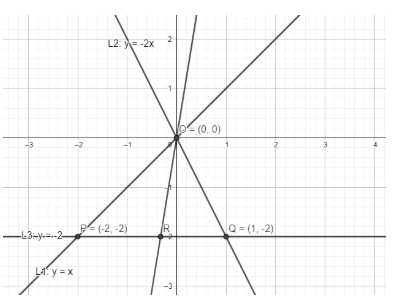
Find the coordinates of P:
As we know P is the intersection point of $y-x=0$ and $y=-2$.
By substituting value of y into 1st equation, we get
$-2-x=0$
By adding wit 2 on both sides, we get:
$x\ =\ -2$
By second equation we already have $y\ =\ -2$
So, coordinates of point P are given by $\left( -2,-2 \right)$.
Finding the coordinate of point Q in the question:
Given in question Q is the intersection of $y+2=0$ , $2x+y=0$.
By substituting value of y into second equation, we get
$2x-2\ =\ 0$
By adding 2 on both sides of equation, we get:
$2x\ =\ 2$
By dividing with 2 on both sides if the equations, we get
$x\ =\ 1$
By first equation y value is already fixed to be $y\ =\ -2$.
Coordinates of Q are $=\ \left( 1,-2 \right)$
As given R is on the internal angular bisector, we know bisector divides the side in the ratio of opposite sides
So, we can say
$\dfrac{\text{PR}}{\text{QR}}=\dfrac{\text{OP}}{\text{OQ}}$ …........................................(i)
By using distance formula between $\left( a,b \right)$ and $\left( c,d \right)$is
$d\ =\ \sqrt{{{\left( a-c \right)}^{2}}+{{\left( b-d \right)}^{2}}}$
By using that we get OP, OQ values to be given by:
$\text{OP}\ =\ \sqrt{{{2}^{2}}+{{2}^{2}}}\ =\ 2\sqrt{2}$, $\text{OQ}\ =\ \sqrt{1+{{2}^{2}}}\ =\ \sqrt{5}$
By equation (i) we can say that $\dfrac{\text{PR}}{\text{QR}}=\dfrac{2\sqrt{2}}{\sqrt{5}}$.
Angle bisector does not give similar triangles in this case.
So, statemtent-1 is true but statement-2 is false.
Hence, option (c) is correct

Note: As you know bisectors divide in the ratio of corresponding sides. So, $\text{OP}:\text{OQ}$ must be written, don't confuse and write $\text{OQ}:\text{OP}$ it is wrong. Be careful while substituting one equation into another by eliminating the other variable because in this method many students confuse keeping the variable value which may lead to wrong answers.