Question

Lines ${{L}_{1}}:\dfrac{x-6}{3}=\dfrac{y-4}{2}=z-2$ and ${{L}_{2}}:\dfrac{x-8}{4}=y-2=\dfrac{z-4}{2}$ meets plane $\pi :\overrightarrow{r}\cdot (2\widehat{i}+\widehat{j}-\widehat{k})=7$at points $A,B$ then find area of triangle formed by the lines ${{L}_{1}},{{L}_{2}}$ and $AB$ is :
A). $\dfrac{7}{2}\sqrt{\dfrac{19}{2}}$
B). $\sqrt{\dfrac{19}{2}}$
C). $\dfrac{\sqrt{11}}{4}$
D). $6\sqrt{5}$

Answer 1

First of all assume the point of intersection of both the lines be $\lambda$ and $\mu$after that find out the value of $\lambda$ and $\mu$ by equating the equations, then find out the value of plane of line by applying vector dot product and we can find out the point of intersection of $A$ and $B$ then find out the area of triangle and check which option is correct in the above given options.

Complete step-by-step solution:
We have given two lines:
$\Rightarrow {{L}_{1}}:\dfrac{x-6}{3}=\dfrac{y-4}{2}=z-2$ mark it as equation $(1)$
$\Rightarrow {{L}_{2}}:\dfrac{x-8}{4}=y-2=\dfrac{z-4}{2}$ mark it as equation $(2)$
Let the point of intersection for equation $(1)$be $\lambda$
Now according to equation $(1)$ we will find out the values of $x,y,z$
$\Rightarrow \dfrac{x-6}{3}=\lambda$
$\Rightarrow x-6=3\lambda$
$\Rightarrow x=3\lambda +6$ mark it as equation $(3)$
Similarly find out the value of $y$
$\Rightarrow \dfrac{y-4}{2}=\lambda$
$\Rightarrow y-4=2\lambda$
$\Rightarrow y=2\lambda +4$ mark it as equation $(4)$
Now find the value of $z$
$\Rightarrow z-2=\lambda$
$\Rightarrow z=\lambda +2$ mark it as equation $(5)$
Let the point of intersection for equation $(2)$be $\mu$
Now according to equation $(2)$ we will find out the values of $x,y,z$
$\Rightarrow \dfrac{x-8}{4}=\mu$
$\Rightarrow x-8=4\mu$
$\Rightarrow x=4\mu +8$ mark it as equation $(6)$
Similarly find out the value of $y$
$\Rightarrow y-2=\mu$
$\Rightarrow y=\mu +2$ mark it as equation $(7)$
Now find the value of $z$
$\Rightarrow \dfrac{z-4}{2}=\mu$
$\Rightarrow z-4=2\mu$
$\Rightarrow z=2\mu +4$ mark it as equation $(8)$
Equating the equation $(3)$ and $(6)$ we get:
$\Rightarrow 3\lambda +6=4\mu +8$
$\Rightarrow 3\lambda -4\mu =8-6$
$\Rightarrow 3\lambda -4\mu =2$ mark it as equation $(9)$
Equating the equation $(4)$ and $(7)$ we get:
$\Rightarrow 2\lambda +4=\mu +2$
$\Rightarrow 2\lambda -\mu =2-4$
$\Rightarrow 2\lambda -\mu =-2$ mark it as equation $(10)$
Now to find the value of $\lambda$ we will multiply equation $(10)$ by $4$ on both sides, then subtract it from equation $(9)$ we will get:
$\Rightarrow \left( 2\lambda -\mu \right)\times 4=-2\times 4$
$\Rightarrow 8\lambda -4\mu =-8$
Now subtract equation $(9)$ from it:
$\Rightarrow 8\lambda -4\mu -\left( 3\lambda -4\mu \right)=-8-2$
$\Rightarrow 8\lambda -4\mu -3\lambda +4\mu =-10$
$\Rightarrow 5\lambda =-10$
$\Rightarrow \lambda =-\dfrac{10}{5}$
$\Rightarrow \lambda =-2$
Hence the point of intersection will be $C(0,0,0)$
We have given $\pi :\overrightarrow{r}\cdot (2\widehat{i}+\widehat{j}-\widehat{k})=7$
As we know that $\overrightarrow{r}=x\widehat{i}+y\widehat{j}+z\widehat{k}$ , put the value of $\overrightarrow{r}$ we get:
$\Rightarrow x\widehat{i}+y\widehat{j}+z\widehat{k}\cdot (2\widehat{i}+\widehat{j}-\widehat{k})=7$
Apply dot product:
$\Rightarrow 2x+y-z=7$
We will find the intersection point for ${{L}_{1}}$ by putting the values of $x,y,z$ from equation $(3),(4),(5)$
$\Rightarrow 2x+y-z=7$
$\Rightarrow 2\left( 3\lambda +6 \right)+2\lambda +4-\left( \lambda +2 \right)=7$
$\Rightarrow 6\lambda +12+2\lambda +4-\lambda -2=7$
$\Rightarrow 7\lambda =-7$
$\Rightarrow \lambda =-1$
Point $A$ will be: $\left( 3\lambda +6,2\lambda +4,\lambda +2 \right)$
Put the value of $\lambda$ we get:
$\Rightarrow A(3,2,1)$
We will find the intersection point for ${{L}_{2}}$ by putting the values of $x,y,z$ from equation $(6),(7),(8)$
$\Rightarrow 2x+y-z=7$
$\Rightarrow 2\left( 4\mu +8 \right)+\mu +2-\left( 2\mu +4 \right)=7$
$\Rightarrow 8\mu +16+\mu +2-2\mu -4=7$
$\Rightarrow 7\mu =-7$
$\Rightarrow \mu =-1$
Point $B$ will be: $\left( 4\mu +8,\mu +2,2\mu +4 \right)$
Put the value of $\mu$ we get:
$\Rightarrow B(4,1,2)$
Hence to find the area of triangle will be:

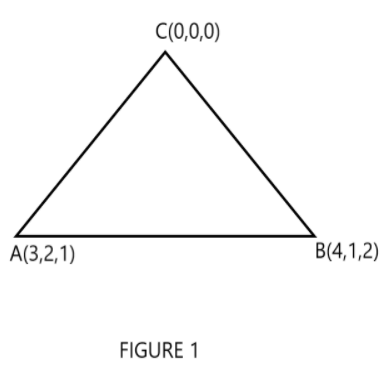
If we write it in vector form then:
$\Rightarrow \overrightarrow{AC}=3\widehat{i}+2\widehat{j}+\widehat{k}$
$\Rightarrow \overrightarrow{BC}=4\widehat{i}+\widehat{j}+2\widehat{k}$
$\Rightarrow \text{Area of triangle=}\dfrac{1}{2}\left| \overrightarrow{AC}\times \overrightarrow{BC} \right|$
Now we will find the value of $\overrightarrow{AC}\times \overrightarrow{BC}$

& \widehat{i}\text{ }\widehat{j}\text{ }\widehat{k} \\\ & 3\text{ }2\text{ }1 \\\ & 4\text{ }1\text{ }2 \\\ \end{aligned} \right|$$ $$=3\widehat{i}-\widehat{j}(2)+\widehat{k}(-5)$$ $$= 3\widehat{i}-2\widehat{j}-5\widehat{k}$$ $$\Rightarrow \left| \overrightarrow{AC}\times \overrightarrow{BC} \right|=\sqrt{9+4+25}$$ $$\Rightarrow \left| \overrightarrow{AC}\times \overrightarrow{BC} \right|=\sqrt{38}$$ Therefore Area of triangle $$ABC$$ will be $$\Rightarrow \dfrac{1}{2}\times \sqrt{38}$$ $$= \dfrac{\sqrt{38}}{2}$$ $$= \dfrac{\sqrt{2}\times \sqrt{19}}{2}$$ $$= \dfrac{\sqrt{2}\times \sqrt{19}}{2}\times \dfrac{\sqrt{2}}{\sqrt{2}}$$ $$= \dfrac{2\times \sqrt{19}}{2\sqrt{2}}$$ $$=\sqrt{\dfrac{19}{2}}$$ **Hence option $$(B)$$ is correct as the area of the triangle is $$\sqrt{\dfrac{19}{2}}$$.** **Note:** Students you know that the total of a triangle's interior angles is always 180o, regardless of how the triangle is created and no matter how a triangle is made, it can always be broken into two right triangles. Any of a triangle's sides is shorter than the total of the other two sides.