Question

Lines are drawn parallel to the line 4x-3y+2 = 0 at a distance of $\dfrac{3}{5}$ from the origin. The which of the following points lies on any one of these lines?
[a] $\left( \dfrac{-1}{4},\dfrac{2}{3} \right)$
[b] $\left( \dfrac{1}{4},\dfrac{2}{3} \right)$
[c] $\left( -\dfrac{1}{4},-\dfrac{2}{3} \right)$
[d] $\left( \dfrac{1}{4},\dfrac{1}{3} \right)$

Answer 1

Use the fact that the slope of the line $Ax+By+C=0$ is given by $m=\dfrac{-A}{B}$. Hence find the slope of the line 4x-3y+2 = 0. Use the fact that the equation of a line parallel to another line of slope m is given by $y=mx+c$. Use the fact that the distance of a line from origin can be found by converting the equation of line to normal form i.e. $x\cos \alpha +y\sin \alpha =p,p\ge 0$. Hence find the equation of the lines parallel to the line 4x-3y+2 and at a distance of $\dfrac{3}{5}$ from the origin

Complete step by step answer:

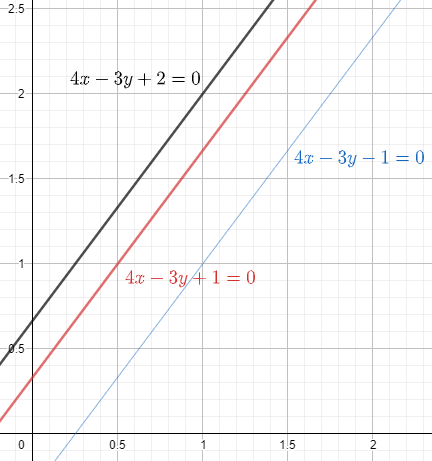
Lines in blue and red are at a distance of $\dfrac{3}{5}$ from origin. The black line is the line 4x-3y+2 = 0
We know that the slope of the line $Ax+By+C=0$ is given by $m=\dfrac{-A}{B}$.
Hence, we have
The slope of the line 4x-3y+2 = 0 is $\dfrac{-4}{-3}=\dfrac{4}{3}$
We know that any line parallel to a line of slope of m is given by y = mx + c
We know that for converting the equation of the line $Ax+By=C$ into normal form, we divide both sides by $\sqrt{{{A}^{2}}+{{B}^{2}}}$
Hence, we have
Equation of a line parallel to the line 4x-3y+2 = 0 is $y=\dfrac{4x}{3}+c$
Dividing both sides by $\sqrt{1+\dfrac{{{4}^{2}}}{{{3}^{2}}}}$, we get
$\dfrac{y}{\sqrt{1+\dfrac{{{4}^{2}}}{{{3}^{2}}}}}-\dfrac{\dfrac{4}{3}x}{\sqrt{1+\dfrac{{{4}^{2}}}{{{3}^{2}}}}}=\dfrac{c}{\sqrt{1+\dfrac{{{4}^{2}}}{{{3}^{2}}}}}$ which is the equation of the line in normal form.
Hence the distance of the line from the origin is $\dfrac{\left| c \right|}{\sqrt{1+\dfrac{{{4}^{2}}}{{{3}^{2}}}}}=\dfrac{3\left| c \right|}{5}$
But given that the distance of the line from the origin is $\dfrac{3}{5}$
Hence, we have
$\begin{aligned} & \dfrac{3\left| c \right|}{5}=\dfrac{3}{5} \\\ & \Rightarrow c=\pm 1 \\\ \end{aligned}$
Hence, the equation of the line is
$y=\dfrac{4}{3}x\pm 1$
When $x=\dfrac{-1}{4}$, we have
$y=\dfrac{-1}{3}\pm 1=\dfrac{2}{3},\dfrac{-4}{3}$
Hence the points $\left( \dfrac{-1}{4},\dfrac{2}{3} \right),\left( -\dfrac{1}{4},\dfrac{-4}{3} \right)$ lie on one of the two possible lines.
Similarly, when $x=\dfrac{1}{4}$, we have
$y=\dfrac{-2}{3},\dfrac{4}{3}$
Hence, the points $\left( \dfrac{1}{4},\dfrac{-2}{3} \right),\left( \dfrac{1}{4},\dfrac{4}{3} \right)$ lie on one of the two possible lines.

So, the correct answer is “Option A”.

Note: [1] In this question many students make mistakes in solving the equation involving modulus. It must be noted that the solution of the equation $\left| x \right|=a,a\ge 0$ is $x=\pm a$. If we take only x = a, then the solution x = -a is lost and hence we arrive at incorrect conclusion