Question

Line $y=mx+c$ cuts the curve ${{y}^{2}}=4ax$ at A and B. Find the equation of circle with AB as diameter.

Answer 1

Hint: In the above equation first of all we have to find the point A and B by solving the equation of line and the curve and then we will use the diametric form of equation for a circle having endpoints $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ given as follows:
$\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)+\left( y-{{y}_{1}} \right)\left( y-{{y}_{2}} \right)=0$

Complete step-by-step answer:
We have been given the line $y=mx+c$ cuts the curve ${{y}^{2}}=4ax$ which is a parabola at A and B as shown as follows:

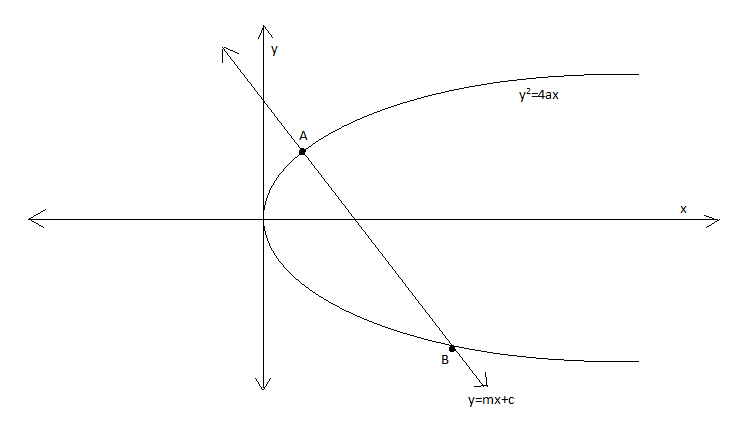
In order to find the points A and B we will substitute the value of Y from the equation of line to the curve.

& \Rightarrow {{\left( mx +c\right)}^{2}}=4ax \\\ & \Rightarrow {{\left( mx \right)}^{2}}+2\left( mx \right).c+{{c}^{2}}=4ax \\\ & \Rightarrow {{m}^{2}}{{x}^{2}}+2mcx+{{c}^{2}}-4ax=0 \\\ & \Rightarrow {{m}^{2}}{{x}^{2}}+2mcx-4ax+{{c}^{2}}=0 \\\ & \Rightarrow {{m}^{2}}{{x}^{2}}+\left( 2mc-4a \right)x+{{c}^{2}}=0 \\\ \end{aligned}$$ We know that the roots of a quadratic equation $$p{{x}^{2}}+bx+k$$ is given by, $$x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4pk}}{2p}$$ So for the above equation, we get as follows: $$p={{m}^{2}},b=\left( 2mc-4a \right),k={{c}^{2}}$$ $$\begin{aligned} & \Rightarrow x=\dfrac{-\left( 2mc-4a \right)\pm \sqrt{\left( 2mc-4{{a}^{2}} \right)-4{{m}^{2}}{{c}^{2}}}}{2{{m}^{2}}} \\\ & \Rightarrow x=\dfrac{-2mc+4a\pm \sqrt{{{\left( 2mc \right)}^{2}}+{{\left( 4a \right)}^{2}}-2\left( 2mc \right)\left( 4a \right)-4{{m}^{2}}{{c}^{2}}}}{2{{m}^{2}}} \\\ & \Rightarrow x=\dfrac{-2mc+4a\pm \sqrt{4{{m}^{2}}{{c}^{2}}+16{{a}^{2}}-16mca-4{{m}^{2}}{{c}^{2}}}}{2{{m}^{2}}} \\\ & \Rightarrow x=\dfrac{-2mc+4a\pm \sqrt{16{{a}^{2}}-16mca}}{2{{m}^{2}}} \\\ \end{aligned}$$ So we get $${{x}_{1}}=\dfrac{-2mc+4a+\sqrt{16{{a}^{2}}-16mca}}{2{{m}^{2}}}$$ and $${{x}_{2}}=\dfrac{-2mc+4a-\sqrt{16{{a}^{2}}-16mca}}{2{{m}^{2}}}$$ On substituting these values in the equation we get as follows: For $${{x}_{1}}$$ we get as follows: $$\begin{aligned} & {{y}_{1}}=m\left( \dfrac{-2mc+4a+\sqrt{16{{a}^{2}}-16mca}}{2{{m}^{2}}} \right)+c \\\ & {{y}_{1}}=\dfrac{-2mc+4a+\sqrt{16{{a}^{2}}-16mca}}{2m}+c \\\ & {{y}_{1}}=\dfrac{-2mc+4a+\sqrt{16{{a}^{2}}-16mca}+2mc}{2m} \\\ & {{y}_{1}}=\dfrac{4a+\sqrt{16{{a}^{2}}-16mca}}{2m} \\\ \end{aligned}$$ For $${{x}_{2}}$$ we get as follows: $$\begin{aligned} & {{y}_{2}}=m\left( \dfrac{-2mc+4a-\sqrt{16{{a}^{2}}-16mca}}{2{{m}^{2}}} \right)+c \\\ & {{y}_{2}}=\dfrac{-2mc+4a-\sqrt{16{{a}^{2}}-16mca}+2mc}{2{{m}^{2}}} \\\ & {{y}_{2}}=\dfrac{-2mc+2mc+4a-\sqrt{16{{a}^{2}}-16mca}}{2{{m}^{2}}} \\\ & {{y}_{2}}=\dfrac{4a-\sqrt{16{{a}^{2}}-16mca}}{2{{m}^{2}}} \\\ \end{aligned}$$ Thus the point A is $$\left( {{x}_{1}},{{y}_{1}} \right)$$ and B is $$\left( {{x}_{2}},{{y}_{2}} \right)$$. We have been asked to find the equation of a circle with AB as diameter and we know that if a circle has diameter endpoints $$\left( {{x}_{1}},{{y}_{1}} \right)$$ and $$\left( {{x}_{2}},{{y}_{2}} \right)$$ then the equation of circle is as follows: $$\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)+\left( y-{{y}_{1}} \right)\left( y-{{y}_{2}} \right)=0$$ On substituting the values of $${{x}_{1}},{{x}_{2}},{{y}_{1}},{{y}_{2}}$$ we get as follows: $$\begin{aligned} & \Rightarrow \left( x-\dfrac{-2mc+4a+\sqrt{16{{a}^{2}}-16mca}}{2{{m}^{2}}} \right)\left( x-\dfrac{-2mc+4a-\sqrt{16{{a}^{2}}-16mca}}{2{{m}^{2}}} \right)+ \\\ & \left( y-\dfrac{4a+\sqrt{16{{a}^{2}}-16mca}}{2m} \right)\left( y-\dfrac{4a-\sqrt{16{{a}^{2}}-16mca}}{2m} \right)=0 \\\ & \Rightarrow \left( x-\dfrac{-2mc+4a+4\sqrt{{{a}^{2}}-mca}}{2{{m}^{2}}} \right)\left( x-\dfrac{-2mc+4a-4\sqrt{{{a}^{2}}-mca}}{2{{m}^{2}}} \right)+ \\\ & \left( y-\dfrac{4a+4\sqrt{{{a}^{2}}-mca}}{2m} \right)\left( y-\dfrac{4a-4\sqrt{{{a}^{2}}-mca}}{2m} \right)=0 \\\ & \Rightarrow \left[ x-\dfrac{-2\left( -mc+2a+2\sqrt{{{a}^{2}}-mca} \right)}{2{{m}^{2}}} \right]\left[ x-\dfrac{2\left( -mc+2a-2\sqrt{{{a}^{2}}-mca} \right)}{2{{m}^{2}}} \right]+ \\\ & \left[ y-\dfrac{2\left( 2a+2\sqrt{{{a}^{2}}-mca} \right)}{2m} \right]\left[ y-\dfrac{2\left( 2a-2\sqrt{{{a}^{2}}-mca} \right)}{2m} \right]=0 \\\ & \Rightarrow \left( x-\dfrac{-mc+2a+2\sqrt{{{a}^{2}}-mca}}{{{m}^{2}}} \right)\left( x-\dfrac{-mc+2a-2\sqrt{{{a}^{2}}-mca}}{{{m}^{2}}} \right)+ \\\ & \left( y-\dfrac{2a+2\sqrt{{{a}^{2}}-mca}}{m} \right)\left( y-\dfrac{2a-2\sqrt{{{a}^{2}}-mca}}{m} \right)=0 \\\ \end{aligned}$$ Now to make simplification easier, let us suppose, $$-mc+2a=\alpha ,2\sqrt{{{a}^{2}}-mca}=\beta ,w=2a$$ On replacing these values, we get as follows: $$\begin{aligned} & \Rightarrow \left( x-\dfrac{\alpha +\beta }{{{m}^{2}}} \right)\left( x-\dfrac{\alpha -\beta }{{{m}^{2}}} \right)+\left( y-\dfrac{w+\beta }{m} \right)\left( y-\dfrac{w-\beta }{m} \right)=0 \\\ & \Rightarrow \left( x-\dfrac{\alpha }{{{m}^{2}}}-\dfrac{\beta }{{{m}^{2}}} \right)\left( x-\dfrac{\alpha }{{{m}^{2}}}+\dfrac{\beta }{{{m}^{2}}} \right)+\left( y-\dfrac{w}{m}-\dfrac{\beta }{m} \right)\left( y-\dfrac{w}{m}+\dfrac{\beta }{m} \right)=0 \\\ \end{aligned}$$ Now by using the identity $$\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$$ we get as follows: $$\Rightarrow {{\left( x-\dfrac{\alpha }{{{m}^{2}}} \right)}^{2}}-{{\left( \dfrac{\beta }{{{m}^{2}}} \right)}^{2}}+{{\left( y-\dfrac{w}{m} \right)}^{2}}-{{\left( \dfrac{w}{m} \right)}^{2}}=0$$ Now by using the identity $${{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}$$ we get as follows: $$\Rightarrow {{x}^{2}}-\dfrac{2x\alpha }{{{m}^{2}}}+{{\left( \dfrac{\alpha }{{{m}^{2}}} \right)}^{2}}-\dfrac{{{\beta }^{2}}}{{{m}^{4}}}+{{y}^{2}}-\dfrac{2yw}{m}+\dfrac{{{w}^{2}}}{{{m}^{2}}}-\dfrac{{{w}^{2}}}{{{m}^{2}}}=0$$ On rearranging the terms, we get as follows: $$\Rightarrow {{x}^{2}}+{{y}^{2}}-\dfrac{2x\alpha}{{{m}^{2}}}-\dfrac{2yw}{m}+\dfrac{{{\alpha }^{2}}-{{\beta }^{2}}}{{{m}^{4}}}+\dfrac{{{w}^{2}}-{{\beta }^{2}}}{{{m}^{2}}}=0$$ Now substituting the value of $$\alpha ,\beta ,w$$ we get as follows: $$\begin{aligned} & \Rightarrow {{x}^{2}}+{{y}^{2}}-\dfrac{2x}{{{m}^{2}}}\left( -mc+2a \right)-\dfrac{2y}{m}\left( 2a \right)+\dfrac{{{\left( -mc+2a \right)}^{2}}-\left( 2\sqrt{{{a}^{2}}-mca} \right)}{{{m}^{4}}}+ \\\ & \dfrac{{{\left( 2a \right)}^{2}}-{{\left( 2\sqrt{{{a}^{2}}-mca} \right)}^{2}}}{{{m}^{2}}}=0 \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}-\dfrac{2\left( -mc+2a \right)}{{{m}^{2}}}x-\dfrac{4a}{m}y+\dfrac{{{m}^{2}}{{c}^{2}}+4{{a}^{2}}-4amc-4{{a}^{2}}+4amc}{{{m}^{4}}}+ \\\ & \dfrac{4{{a}^{2}}-4{{a}^{2}}-4mca}{{{m}^{2}}}=0 \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}-\dfrac{2\left( 2a-mc \right)}{{{m}^{2}}}x-\dfrac{4a}{m}y+\dfrac{{{m}^{2}}{{c}^{2}}}{{{m}^{4}}}+\dfrac{4mca}{{{m}^{2}}}=0 \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}-2\left( \dfrac{2a-mc}{{{m}^{2}}} \right)x-\left( \dfrac{4a}{m} \right)y+\dfrac{{{c}^{2}}}{{{m}^{2}}}+\dfrac{4ac}{m}=0 \\\ \end{aligned}$$ Note: Be careful while calculation and take care of signs and values in each step of calculation. We can also solve it by finding the center of the circle through the endpoints of diameter using the midpoint formula and the radius by distance formula and thus write the equation in center and radius form.