Question
Question: $\lim_{x\to\infty}\frac{d}{dx}\left(\frac{8x^2+bx+c}{4x+f}\right)=2m$, then $\lim_{x\to m^+}2^{\frac...
limx→∞dxd(4x+f8x2+bx+c)=2m, then limx→m+22(1−x)1=
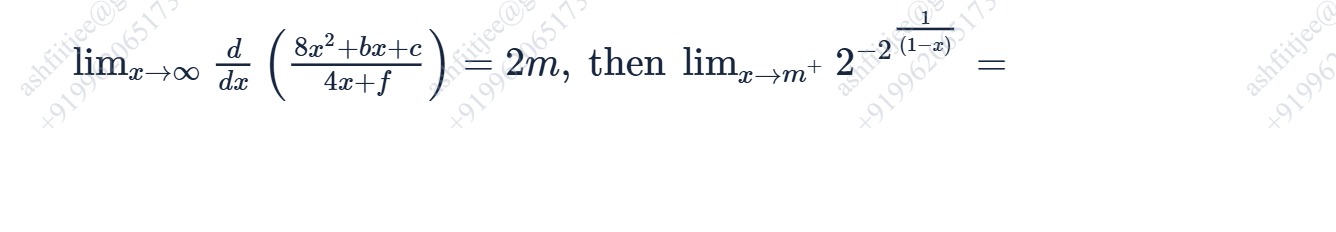
0
Solution
First, we need to evaluate the derivative of the function y=4x+f8x2+bx+c with respect to x.
Using the quotient rule, dxd(vu)=v2u′v−uv′, where u=8x2+bx+c and v=4x+f.
u′=16x+b and v′=4.
dxd(4x+f8x2+bx+c)=(4x+f)2(16x+b)(4x+f)−(8x2+bx+c)(4)
Expanding the numerator:
(16x+b)(4x+f)−4(8x2+bx+c)=(64x2+16xf+4bx+bf)−(32x2+4bx+4c)
=64x2+16xf+4bx+bf−32x2−4bx−4c
=32x2+16xf+bf−4c
The derivative is:
dxd(4x+f8x2+bx+c)=(4x+f)232x2+16xf+bf−4c=16x2+8xf+f232x2+16xf+bf−4c
Next, we evaluate the limit of this derivative as x→∞.
limx→∞16x2+8xf+f232x2+16xf+bf−4c
This is the limit of a rational function where the degree of the numerator and the denominator are equal (both are 2). The limit as x→∞ is the ratio of the leading coefficients.
limx→∞16x2+8xf+f232x2+16xf+bf−4c=1632=2
The problem states that this limit is equal to 2m.
2m=2
Dividing by 2, we get m=1.
Now we need to evaluate the second limit: limx→m+22(1−x)1.
Substitute m=1:
limx→1+22(1−x)1
Let's analyze the exponent 2(1−x)1 as x→1+.
As x→1 from the right side (x>1), the term (1−x) approaches 0 from the negative side (1−x<0).
Let x=1+h, where h→0+.
Then 1−x=1−(1+h)=−h.
The exponent becomes 2(−h)1=−2h1.
As h→0+, 2h→0+, so 2h1→+∞.
Therefore, −2h1→−∞.
The limit becomes:
limh→0+2−2h1=2−∞
We know that 2−∞=2∞1=∞1=0.
So, limx→1+22(1−x)1=0.
