Question

$\lim_{x\to\infty}(2^x+3^x)^{1/x}$

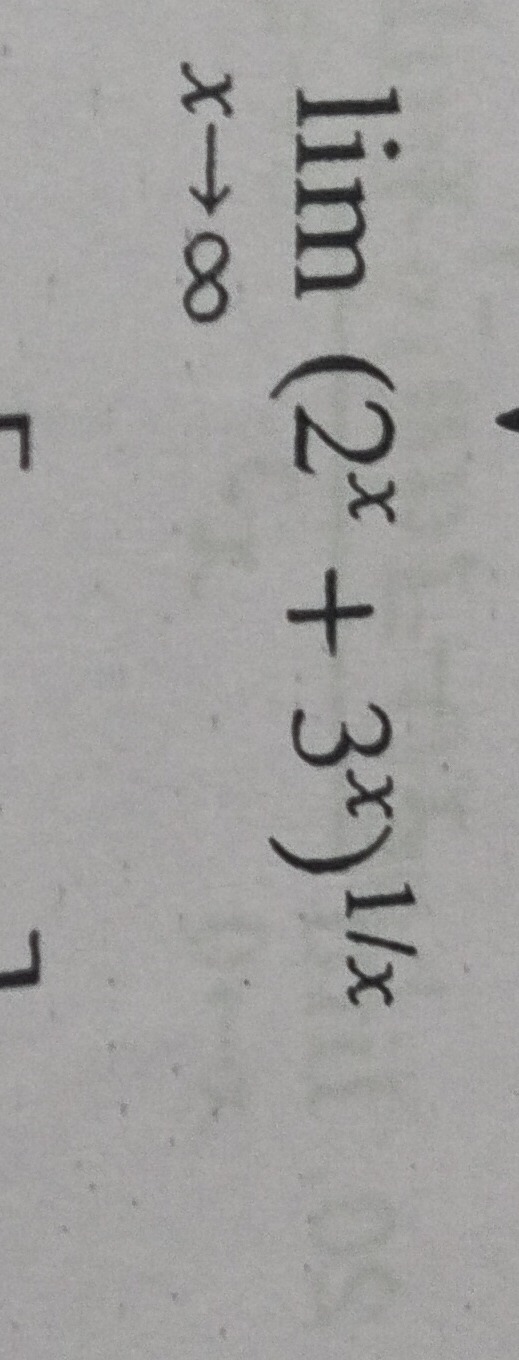
Answer 1

3

Answer 2

The limit is of the indeterminate form $\infty^0$.

Let $L = \lim_{x\to\infty}(2^x+3^x)^{1/x}$.

Consider $\ln L = \lim_{x\to\infty} \frac{\ln(2^x+3^x)}{x}$.

Factor out the dominant term $3^x$: $\ln(2^x+3^x) = \ln(3^x((\frac{2}{3})^x+1)) = x \ln 3 + \ln((\frac{2}{3})^x+1)$.

So, $\ln L = \lim_{x\to\infty} \frac{x \ln 3 + \ln((\frac{2}{3})^x+1)}{x} = \lim_{x\to\infty} (\ln 3 + \frac{\ln((\frac{2}{3})^x+1)}{x})$.

As $x \to \infty$, $(\frac{2}{3})^x \to 0$, so $\ln((\frac{2}{3})^x+1) \to \ln(1) = 0$.

Thus, $\lim_{x\to\infty} \frac{\ln((\frac{2}{3})^x+1)}{x} = \frac{0}{\infty} = 0$.

$\ln L = \ln 3 + 0 = \ln 3$.

$L = e^{\ln 3} = 3$.