Solveeit Logo
Login

Question

Question: $\lim_{x\to\infty} \left( \sqrt{x^2-\frac{4x}{3}} + x + 2 \right)$ is equal to-...

lim⁡x→∞(x2−4x3+x+2)\lim_{x\to\infty} \left( \sqrt{x^2-\frac{4x}{3}} + x + 2 \right) is equal to-

A

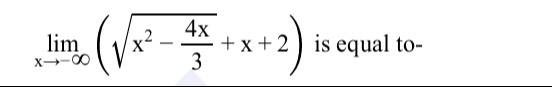
-4/3

B

4/3

C

2/3

D

-2/3

Answer

The limit as x approaches infinity is infinity. However, given the options, it's highly probable there's a typo in the question, and it should be a subtraction. If the question was lim⁡x→∞(x2−4x3−x+2)\lim_{x\to\infty} \left( \sqrt{x^2-\frac{4x}{3}} - x + 2 \right), the answer would be 4/3.

Explanation

Solution

The given limit is lim⁡x→∞(x2−4x3+x+2)\lim_{x\to\infty} \left( \sqrt{x^2-\frac{4x}{3}} + x + 2 \right). As x→∞x \to \infty, x2−4x3≈x2=x\sqrt{x^2-\frac{4x}{3}} \approx \sqrt{x^2} = x. Thus, the expression approaches x+x+2=2x+2x + x + 2 = 2x + 2. As x→∞x \to \infty, 2x+2→∞2x+2 \to \infty. This indicates that the limit is infinity.

However, since the options are finite numerical values, it is highly probable that there is a typo in the question and the expression should have been x2−4x3−x+2\sqrt{x^2-\frac{4x}{3}} - x + 2.

Assuming the question intended to be lim⁡x→∞(x2−4x3−x+2)\lim_{x\to\infty} \left( \sqrt{x^2-\frac{4x}{3}} - x + 2 \right):

  1. Consider the indeterminate form lim⁡x→∞(x2−4x3−x)\lim_{x\to\infty} \left( \sqrt{x^2-\frac{4x}{3}} - x \right).

  2. Rationalize the expression by multiplying and dividing by the conjugate (x2−4x3+x)\left(\sqrt{x^2-\frac{4x}{3}} + x\right):

    lim⁡x→∞(x2−4x3−x)(x2−4x3+x)x2−4x3+x\lim_{x\to\infty} \frac{\left(\sqrt{x^2-\frac{4x}{3}} - x\right)\left(\sqrt{x^2-\frac{4x}{3}} + x\right)}{\sqrt{x^2-\frac{4x}{3}} + x} =lim⁡x→∞(x2−4x3)−x2x2−4x3+x=lim⁡x→∞−4x3x2−4x3+x= \lim_{x\to\infty} \frac{(x^2-\frac{4x}{3}) - x^2}{\sqrt{x^2-\frac{4x}{3}} + x} = \lim_{x\to\infty} \frac{-\frac{4x}{3}}{\sqrt{x^2-\frac{4x}{3}} + x}

  3. Factor out xx from the denominator:

    =lim⁡x→∞−4x3x2(1−43x)+x=lim⁡x→∞−4x3x1−43x+x(since x>0 for x→∞)= \lim_{x\to\infty} \frac{-\frac{4x}{3}}{\sqrt{x^2(1-\frac{4}{3x})} + x} = \lim_{x\to\infty} \frac{-\frac{4x}{3}}{x\sqrt{1-\frac{4}{3x}} + x} \quad (\text{since } x>0 \text{ for } x \to \infty) =lim⁡x→∞−4x3x(1−43x+1)=lim⁡x→∞−431−43x+1= \lim_{x\to\infty} \frac{-\frac{4x}{3}}{x\left(\sqrt{1-\frac{4}{3x}} + 1\right)} = \lim_{x\to\infty} \frac{-\frac{4}{3}}{\sqrt{1-\frac{4}{3x}} + 1}

  4. As x→∞x \to \infty, 43x→0\frac{4}{3x} \to 0. So, 1−43x→1−0=1\sqrt{1-\frac{4}{3x}} \to \sqrt{1-0} = 1.

    =−431+1=−432=−23= \frac{-\frac{4}{3}}{1 + 1} = \frac{-\frac{4}{3}}{2} = -\frac{2}{3}

  5. Now add the constant term +2+2 from the original (modified) expression:

    lim⁡x→∞(x2−4x3−x+2)=−23+2=−2+63=43\lim_{x\to\infty} \left( \sqrt{x^2-\frac{4x}{3}} - x + 2 \right) = -\frac{2}{3} + 2 = \frac{-2+6}{3} = \frac{4}{3}