Question

$\lim_{x\to1} \frac{\sqrt[n]{x}-1}{\sqrt[m]{x}-1}$(m and n integers) is equal to:

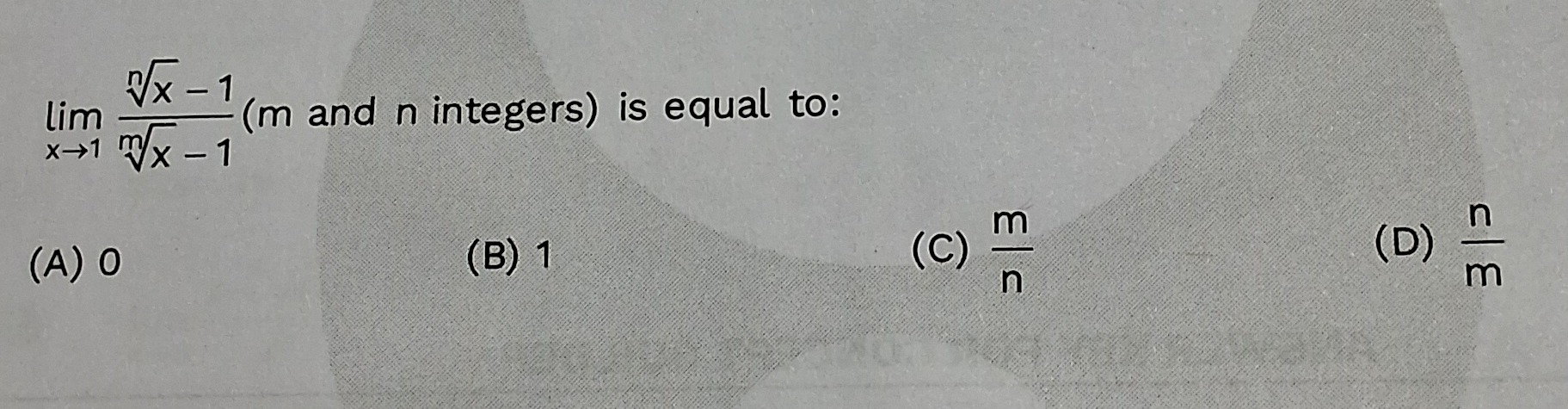
• A. 0
• B. 1
• C. $\frac{m}{n}$
• D. $\frac{n}{m}$

Answer 1

Answer: (C)

(C)

Answer 2

The limit is of the $\frac{0}{0}$ indeterminate form. Applying L'Hopital's Rule, we differentiate the numerator and the denominator with respect to $x$. The derivative of $x^{1/n}-1$ is $\frac{1}{n}x^{\frac{1}{n}-1}$ and the derivative of $x^{1/m}-1$ is $\frac{1}{m}x^{\frac{1}{m}-1}$. Taking the limit of their ratio as $x \to 1$, we get $\frac{m}{n} \frac{1^{1/n-1}}{1^{1/m-1}} = \frac{m}{n}$.

Alternatively, by substituting $x=1+h$ and dividing numerator and denominator by $h$, the limit transforms into a ratio of two standard limits of the form $\lim_{h\to0} \frac{(1+h)^k-1}{h}=k$, which gives $\frac{1/n}{1/m} = \frac{m}{n}$.