Question
Question: $\lim_{x\to0}\frac{(729)^x-(243)^x-(81)^x+9^x+3^x-1}{x^3}$...
limx→0x3(729)x−(243)x−(81)x+9x+3x−1
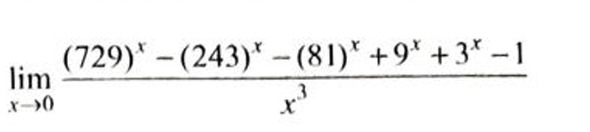
6(\ln 3)^3
Solution
The limit expression can be rewritten using ax=exlna. Let k=ln3. The limit becomes limx→0x3e6kx−e5kx−e4kx+e2kx+ekx−1. This limit can be evaluated using the Taylor expansion of eu=1+u+2!u2+3!u3+… for each term. Upon expansion and collecting terms, the coefficients of x and x2 in the numerator are found to be zero, while the coefficient of x3 is 6k3. Thus, the limit is limx→0x36k3x3=6k3. Substituting k=ln3 gives the result 6(ln3)3. Alternatively, recognizing the limit as 3!f′′′(0) for f(x)=(729)x−(243)x−(81)x+9x+3x−1 and calculating the third derivative at x=0 also yields 36(ln3)3, leading to the limit 636(ln3)3=6(ln3)3. A third method involves substituting a=3x and factoring the numerator as (a−1)3(a+1)(a2+a+1), then using x=ln3lna and the standard limit lima→1lnaa−1=1 to get 6(ln3)3.
