Question
Question: $\lim_{x\to0} \frac{\int_{0}^{x^2} \cos t^2 dt}{x \sin x}$ is equal to...
limx→0xsinx∫0x2cost2dt is equal to
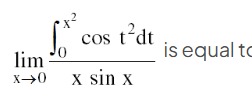
1
Solution
The given limit is limx→0xsinx∫0x2cost2dt.
Step 1: Check the form of the limit. As x→0: Numerator: ∫0x2cost2dt→∫00cost2dt=0. Denominator: xsinx→0⋅sin0=0⋅0=0. The limit is of the indeterminate form 00. Therefore, we can apply L'Hopital's Rule.
Step 2: Apply L'Hopital's Rule for the first time. Let N(x)=∫0x2cost2dt and D(x)=xsinx. We need to find N′(x) and D′(x).
For N′(x), we use the Leibniz integral rule: dxd∫a(x)b(x)h(t)dt=h(b(x))b′(x)−h(a(x))a′(x). Here, h(t)=cost2, a(x)=0, and b(x)=x2. N′(x)=cos((x2)2)⋅dxd(x2)−cos(02)⋅dxd(0) N′(x)=cos(x4)⋅(2x)−cos(0)⋅0 N′(x)=2xcos(x4)
For D′(x), we use the product rule: dxd(uv)=u′v+uv′. D′(x)=dxd(xsinx)=(1)sinx+x(cosx) D′(x)=sinx+xcosx
Applying L'Hopital's Rule, the limit becomes: limx→0sinx+xcosx2xcos(x4)
Step 3: Check the form of the new limit. As x→0: Numerator: 2(0)cos(04)=0⋅1=0. Denominator: sin0+0cos0=0+0=0. The limit is still of the indeterminate form 00. So, we apply L'Hopital's Rule again.
Step 4: Apply L'Hopital's Rule for the second time. Let N1(x)=2xcos(x4) and D1(x)=sinx+xcosx. We need to find N1′(x) and D1′(x).
For N1′(x), use the product rule: N1′(x)=dxd(2xcos(x4))=2⋅cos(x4)+2x⋅(−sin(x4)⋅dxd(x4)) N1′(x)=2cos(x4)−2xsin(x4)⋅(4x3) N1′(x)=2cos(x4)−8x4sin(x4)
For D1′(x): D1′(x)=dxd(sinx+xcosx)=cosx+(1⋅cosx+x⋅(−sinx)) D1′(x)=cosx+cosx−xsinx D1′(x)=2cosx−xsinx
Applying L'Hopital's Rule again, the limit becomes: limx→02cosx−xsinx2cos(x4)−8x4sin(x4)
Step 5: Evaluate the final limit. As x→0: Numerator: 2cos(04)−8(0)4sin(04)=2cos(0)−0=2(1)−0=2. Denominator: 2cos0−0sin0=2(1)−0=2. The limit evaluates to 22=1.
The final answer is 1.
Explanation of the solution: The limit is of the form 00. Apply L'Hopital's Rule twice.
- Differentiate the numerator using Leibniz rule: dxd∫0x2cost2dt=2xcos(x4).
- Differentiate the denominator using product rule: dxd(xsinx)=sinx+xcosx. The limit becomes limx→0sinx+xcosx2xcos(x4), which is still 00.
- Differentiate the new numerator: dxd(2xcos(x4))=2cos(x4)−8x4sin(x4).
- Differentiate the new denominator: dxd(sinx+xcosx)=2cosx−xsinx. The limit becomes limx→02cosx−xsinx2cos(x4)−8x4sin(x4).
- Substitute x=0: 2cos(0)−02cos(0)−0=22=1.
