Question
Question: $\lim_{x\to 1}\left[\frac{x+x^2+x^3+......+x^n-n}{x-1}\right]$...
limx→1[x−1x+x2+x3+......+xn−n]
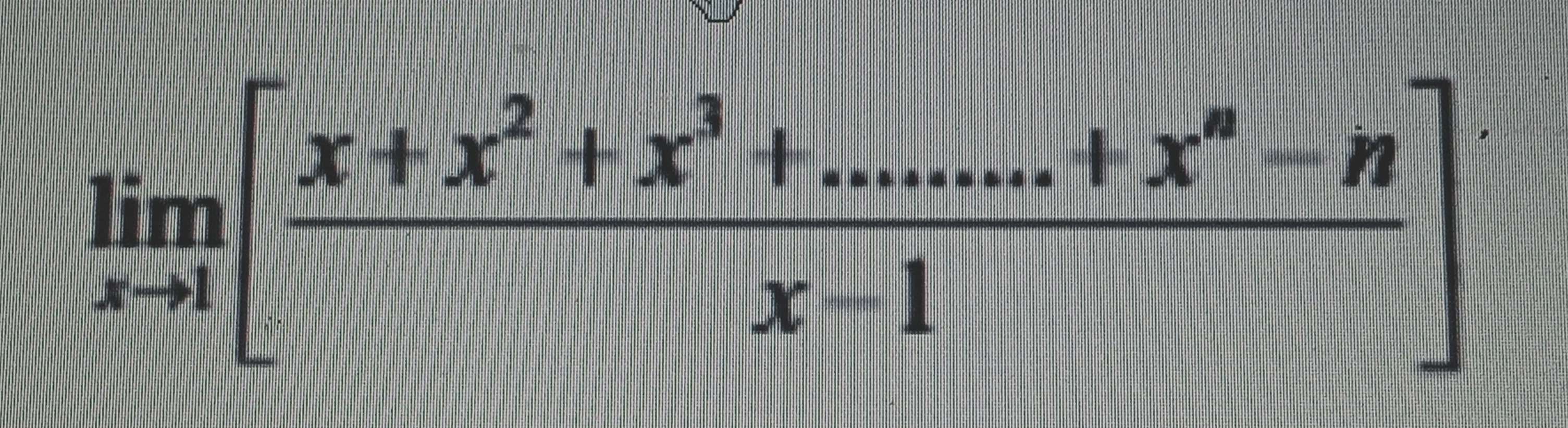
2n(n+1)
Solution
The given limit is limx→1[x−1x+x2+x3+......+xn−n].
Let f(x)=x+x2+x3+......+xn.
Evaluate f(x) at x=1:
f(1)=1+12+13+......+1n=1+1+......+1 (n times) =n.
The given limit can be written as limx→1x−1f(x)−n.
Since f(1)=n, the limit becomes limx→1x−1f(x)−f(1).
This expression is the definition of the derivative of the function f(x) at x=1, which is denoted as f′(1).
To find f′(1), we first find the derivative of f(x) with respect to x.
f(x)=x+x2+x3+......+xn.
Using the power rule for differentiation, dxd(xk)=kxk−1, we differentiate each term:
f′(x)=dxd(x)+dxd(x2)+dxd(x3)+......+dxd(xn)
f′(x)=1⋅x1−1+2⋅x2−1+3⋅x3−1+......+n⋅xn−1
f′(x)=1⋅x0+2⋅x1+3⋅x2+......+n⋅xn−1
f′(x)=1+2x+3x2+......+nxn−1.
Now, evaluate f′(x) at x=1:
f′(1)=1+2(1)+3(1)2+......+n(1)n−1
f′(1)=1+2+3+......+n.
This is the sum of the first n positive integers. The formula for the sum of the first n positive integers is 2n(n+1).
So, f′(1)=2n(n+1).
Therefore, the value of the limit is 2n(n+1).
