Question

$\lim_{x\to 1}\frac{\sqrt[n]{x}-1}{\sqrt[m]{x}-1}$(m and n integers) is equal to:

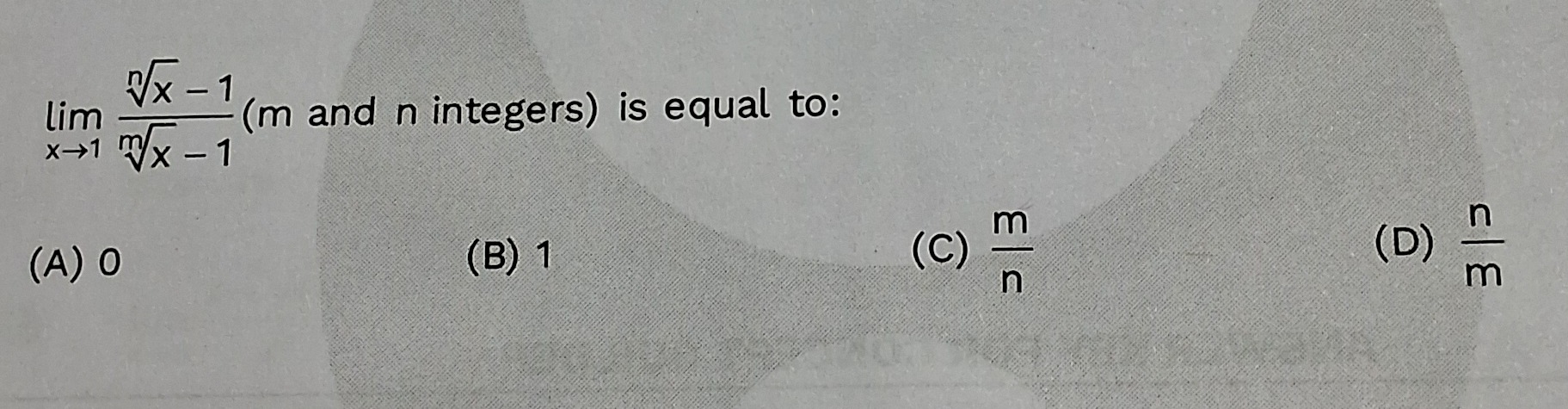
• A. 0
• B. 1
• C. $\frac{m}{n}$
• D. $\frac{n}{m}$

Answer 1

Answer: (C)

$\frac{m}{n}$

Answer 2

The problem requires evaluating the limit:

$$\lim_{x\to 1}\frac{\sqrt[n]{x}-1}{\sqrt[m]{x}-1}$$

where $m$ and $n$ are integers.

Substituting $x=1$ yields the indeterminate form $\frac{0}{0}$, allowing us to use L'Hopital's Rule.

Applying L'Hopital's Rule:

Let $f(x) = x^{1/n} - 1$ and $g(x) = x^{1/m} - 1$. Then:

$f'(x) = \frac{1}{n}x^{\frac{1}{n}-1}$

$g'(x) = \frac{1}{m}x^{\frac{1}{m}-1}$

Thus,

$$\lim_{x\to 1}\frac{f'(x)}{g'(x)} = \lim_{x\to 1}\frac{\frac{1}{n}x^{\frac{1}{n}-1}}{\frac{1}{m}x^{\frac{1}{m}-1}} = \lim_{x\to 1}\frac{m}{n}x^{\frac{1}{n}-\frac{1}{m}}$$

Substituting $x=1$:

$$\frac{m}{n}(1)^{\frac{1}{n}-\frac{1}{m}} = \frac{m}{n}$$

Alternative Method: Using Standard Limit Formula

Rewrite the limit by dividing both numerator and denominator by $(x-1)$:

$$\lim_{x\to 1}\frac{\frac{x^{1/n}-1}{x-1}}{\frac{x^{1/m}-1}{x-1}}$$

Using the standard limit formula $\lim_{x\to a}\frac{x^p - a^p}{x-a} = pa^{p-1}$:

Numerator limit: $\frac{1}{n}$

Denominator limit: $\frac{1}{m}$

Therefore, the original limit is:

$$\frac{\frac{1}{n}}{\frac{1}{m}} = \frac{m}{n}$$

Both methods confirm the result.