Question

$\lim_{x\to 1} \frac{x^{2024}-1}{x^{2022}-1}$

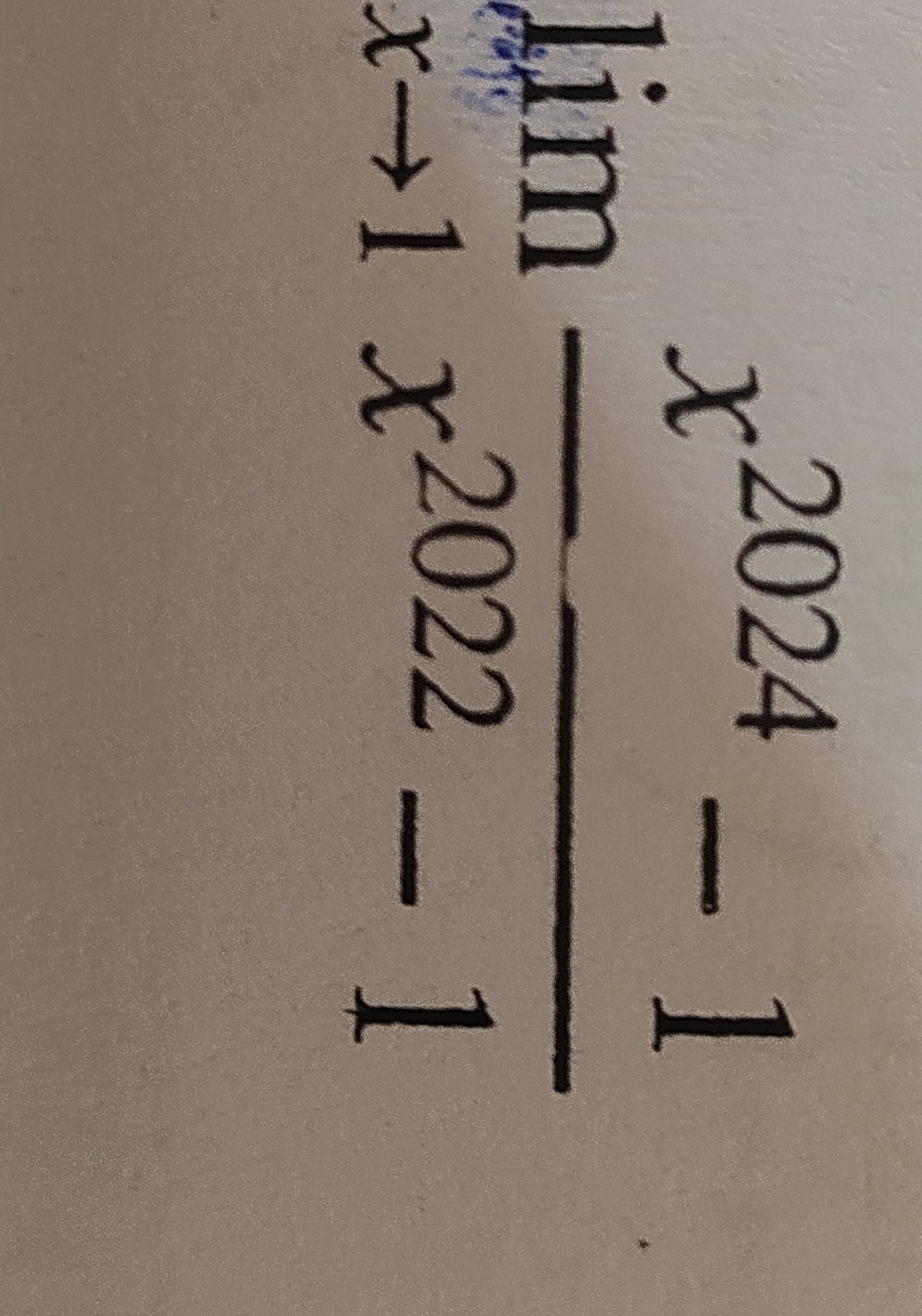
Answer 1

$\frac{1012}{1011}$

Answer 2

The given limit is of the indeterminate form $\frac{0}{0}$ as $x \to 1$. We can evaluate this limit using L'Hopital's Rule or by algebraic manipulation.

Method 1: L'Hopital's Rule

Applying L'Hopital's Rule, we differentiate the numerator and the denominator with respect to $x$:

$$\lim_{x\to 1} \frac{x^{2024}-1}{x^{2022}-1} = \lim_{x\to 1} \frac{\frac{d}{dx}(x^{2024}-1)}{\frac{d}{dx}(x^{2022}-1)} = \lim_{x\to 1} \frac{2024x^{2023}}{2022x^{2021}}$$

Now, substitute $x=1$:

$$\frac{2024(1)^{2023}}{2022(1)^{2021}} = \frac{2024}{2022} = \frac{1012}{1011}$$

Method 2: Algebraic Manipulation

We can factor the numerator and denominator using the difference of powers factorization: $a^n - b^n = (a-b)(a^{n-1} + a^{n-2}b + \dots + ab^{n-2} + b^{n-1})$.

$$x^{2024}-1 = (x-1)(x^{2023} + x^{2022} + \dots + x + 1)$$ $$x^{2022}-1 = (x-1)(x^{2021} + x^{2020} + \dots + x + 1)$$

Substitute these factorizations into the limit expression:

$$\lim_{x\to 1} \frac{(x-1)(x^{2023} + x^{2022} + \dots + x + 1)}{(x-1)(x^{2021} + x^{2020} + \dots + x + 1)}$$

Cancel the common factor $(x-1)$ for $x \neq 1$:

$$\lim_{x\to 1} \frac{x^{2023} + x^{2022} + \dots + x + 1}{x^{2021} + x^{2020} + \dots + x + 1}$$

Now, substitute $x=1$ into the simplified expression. The numerator has 2024 terms, each equal to 1. The denominator has 2022 terms, each equal to 1.

$$\frac{2024}{2022} = \frac{1012}{1011}$$

Thus, the limit is $\frac{1012}{1011}$.