Question
Question: $\lim_{x\to 0}\frac{sinln \frac{2024}{2024-x}}{tan(\frac{2024}{2024-3x}-1)}$...
limx→0tan(2024−3x2024−1)sinln2024−x2024
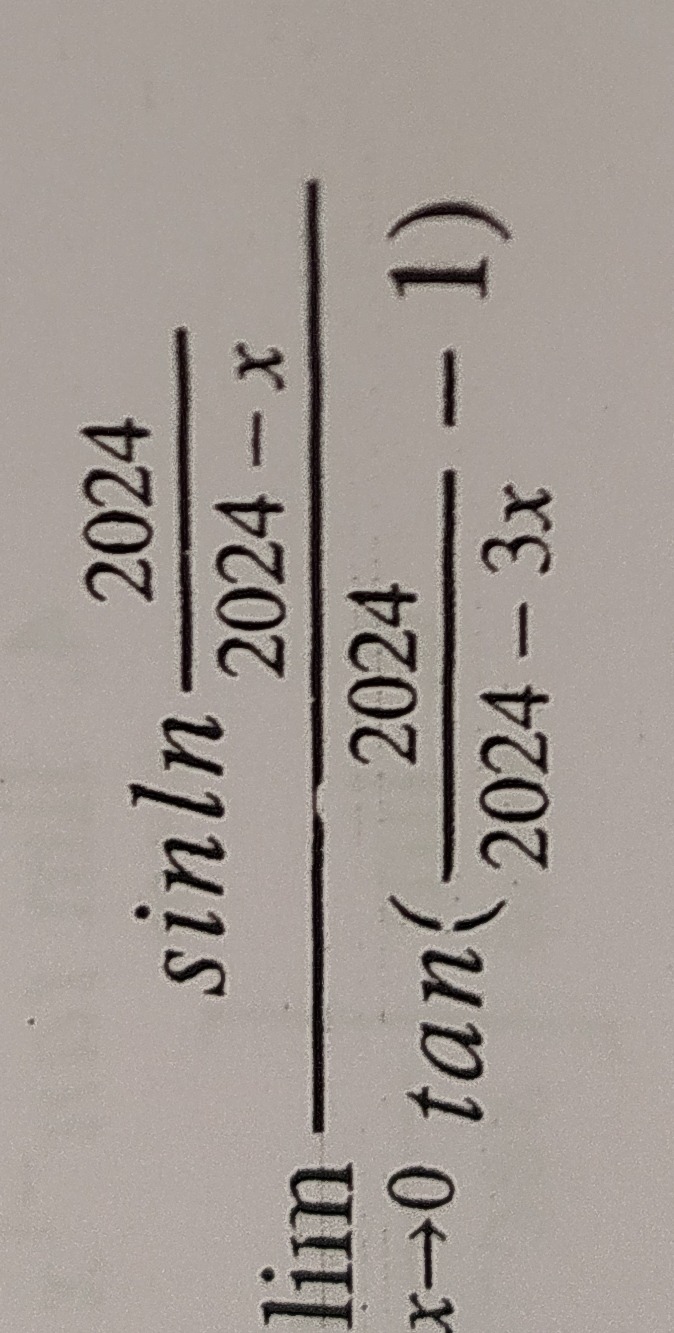
1/3
Solution
The given limit is of the indeterminate form 00. We can use standard limits or L'Hopital's rule.
We use the standard limits: limu→0usinu=1, limu→0utanu=1, and limu→0uln(1+u)=1.
Let's analyze the numerator: sin(ln2024−x2024).
ln2024−x2024=ln(2024−x2024−x+x)=ln(1+2024−xx).
As x→0, 2024−xx→0.
Let u(x)=ln(1+2024−xx). As x→0, u(x)→0.
The numerator is sin(u(x)). We can write this as u(x)sin(u(x))⋅u(x).
limx→0u(x)sin(u(x))=1.
Now consider u(x)=ln(1+2024−xx). Let v(x)=2024−xx. As x→0, v(x)→0.
u(x)=ln(1+v(x)). We can write this as v(x)ln(1+v(x))⋅v(x).
limx→0v(x)ln(1+v(x))=1.
So, the numerator is asymptotically equivalent to v(x)=2024−xx as x→0.
limx→0xsin(ln2024−x2024)=limx→0u(x)sin(u(x))⋅v(x)ln(1+v(x))⋅xv(x)=1⋅1⋅limx→0x2024−xx=limx→02024−x1=20241.
Let's analyze the denominator: tan(2024−3x2024−1).
2024−3x2024−1=2024−3x2024−(2024−3x)=2024−3x3x.
As x→0, 2024−3x3x→0.
Let w(x)=2024−3x3x. As x→0, w(x)→0.
The denominator is tan(w(x)). We can write this as w(x)tan(w(x))⋅w(x).
limx→0w(x)tan(w(x))=1.
So, the denominator is asymptotically equivalent to w(x)=2024−3x3x as x→0.
limx→0xtan(2024−3x2024−1)=limx→0w(x)tan(w(x))⋅xw(x)=1⋅limx→0x2024−3x3x=limx→02024−3x3=20243.
Now, we can evaluate the limit of the ratio:
limx→0tan(2024−3x2024−1)sin(ln2024−x2024)=limx→0xtan(2024−3x2024−1)xsin(ln2024−x2024).
Using the limits we found for the numerator and denominator divided by x:
=limx→0xtan(2024−3x2024−1)limx→0xsin(ln2024−x2024)=3/20241/2024=31.
