Solveeit Logo
Login

Question

Question: $\lim_{x\to 0}\frac{(1+\sin x)^{\frac{1}{2024}}+(1-\tan x)^{\frac{1}{2024}}-2}{x^3}$...

lim⁡x→0(1+sin⁡x)12024+(1−tan⁡x)12024−2x3\lim_{x\to 0}\frac{(1+\sin x)^{\frac{1}{2024}}+(1-\tan x)^{\frac{1}{2024}}-2}{x^3}

Answer

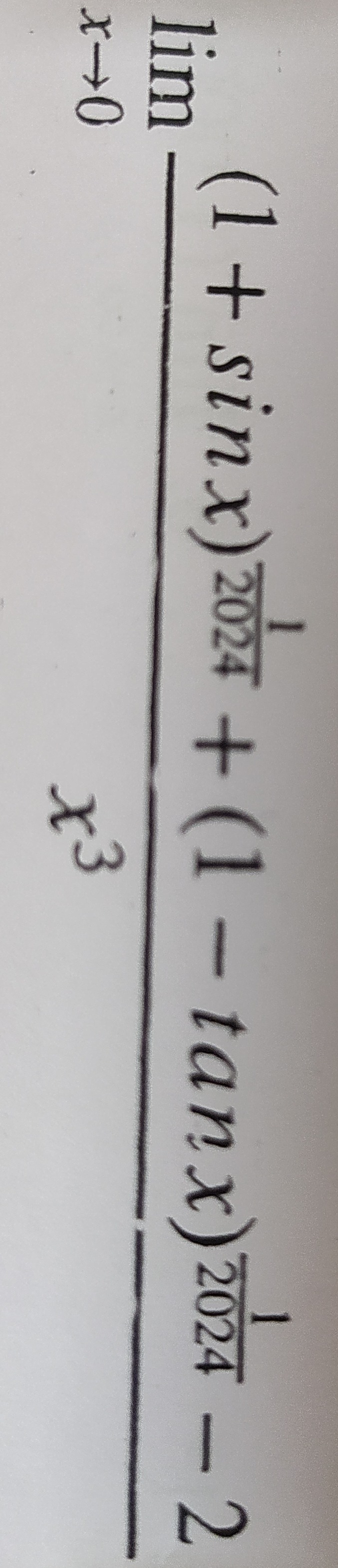
Does not exist

Explanation

Solution

To evaluate the limit lim⁡x→0(1+sin⁡x)12024+(1−tan⁡x)12024−2x3\lim_{x\to 0}\frac{(1+\sin x)^{\frac{1}{2024}}+(1-\tan x)^{\frac{1}{2024}}-2}{x^3}, we will use Taylor series expansions for sin⁡x\sin x, tan⁡x\tan x, and the generalized binomial theorem.

Let n=12024n = \frac{1}{2024}. The generalized binomial expansion for (1+u)n(1+u)^n around u=0u=0 is: (1+u)n=1+nu+n(n−1)2!u2+n(n−1)(n−2)3!u3+O(u4)(1+u)^n = 1 + nu + \frac{n(n-1)}{2!}u^2 + \frac{n(n-1)(n-2)}{3!}u^3 + O(u^4).

We need the Taylor series expansions for sin⁡x\sin x and tan⁡x\tan x around x=0x=0 up to x3x^3: sin⁡x=x−x33!+O(x5)=x−x36+O(x5)\sin x = x - \frac{x^3}{3!} + O(x^5) = x - \frac{x^3}{6} + O(x^5) tan⁡x=x+x33+O(x5)\tan x = x + \frac{x^3}{3} + O(x^5)

Now, let's expand (1+sin⁡x)n(1+\sin x)^n: Let u=sin⁡xu = \sin x. u=x−x36+O(x5)u = x - \frac{x^3}{6} + O(x^5) u2=(sin⁡x)2=(x−x36+O(x5))2=x2−2x(x36)+O(x6)=x2−x43+O(x6)u^2 = (\sin x)^2 = \left(x - \frac{x^3}{6} + O(x^5)\right)^2 = x^2 - 2x\left(\frac{x^3}{6}\right) + O(x^6) = x^2 - \frac{x^4}{3} + O(x^6) u3=(sin⁡x)3=(x−x36+O(x5))3=x3+O(x5)u^3 = (\sin x)^3 = \left(x - \frac{x^3}{6} + O(x^5)\right)^3 = x^3 + O(x^5)

Substitute these into the binomial expansion: (1+sin⁡x)n=1+n(x−x36)+n(n−1)2(x2−x43)+n(n−1)(n−2)6(x3)+O(x4)(1+\sin x)^n = 1 + n\left(x - \frac{x^3}{6}\right) + \frac{n(n-1)}{2}\left(x^2 - \frac{x^4}{3}\right) + \frac{n(n-1)(n-2)}{6}(x^3) + O(x^4) (1+sin⁡x)n=1+nx−n6x3+n(n−1)2x2+n(n−1)(n−2)6x3+O(x4)(1+\sin x)^n = 1 + nx - \frac{n}{6}x^3 + \frac{n(n-1)}{2}x^2 + \frac{n(n-1)(n-2)}{6}x^3 + O(x^4) Rearranging terms by powers of xx: (1+sin⁡x)n=1+nx+n(n−1)2x2+(n(n−1)(n−2)6−n6)x3+O(x4)(1+\sin x)^n = 1 + nx + \frac{n(n-1)}{2}x^2 + \left(\frac{n(n-1)(n-2)}{6} - \frac{n}{6}\right)x^3 + O(x^4) (1+sin⁡x)n=1+nx+n(n−1)2x2+n((n−1)(n−2)−1)6x3+O(x4)(1+\sin x)^n = 1 + nx + \frac{n(n-1)}{2}x^2 + \frac{n((n-1)(n-2) - 1)}{6}x^3 + O(x^4) (1+sin⁡x)n=1+nx+n(n−1)2x2+n(n2−3n+2−1)6x3+O(x4)(1+\sin x)^n = 1 + nx + \frac{n(n-1)}{2}x^2 + \frac{n(n^2-3n+2-1)}{6}x^3 + O(x^4) (1+sin⁡x)n=1+nx+n(n−1)2x2+n(n2−3n+1)6x3+O(x4)(1+\sin x)^n = 1 + nx + \frac{n(n-1)}{2}x^2 + \frac{n(n^2-3n+1)}{6}x^3 + O(x^4) (Equation 1)

Next, let's expand (1−tan⁡x)n(1-\tan x)^n: Let v=−tan⁡xv = -\tan x. v=−(x+x33+O(x5))=−x−x33+O(x5)v = -\left(x + \frac{x^3}{3} + O(x^5)\right) = -x - \frac{x^3}{3} + O(x^5) v2=(−tan⁡x)2=(−x−x33+O(x5))2=x2+2x(x33)+O(x6)=x2+2x43+O(x6)v^2 = (-\tan x)^2 = \left(-x - \frac{x^3}{3} + O(x^5)\right)^2 = x^2 + 2x\left(\frac{x^3}{3}\right) + O(x^6) = x^2 + \frac{2x^4}{3} + O(x^6) v3=(−tan⁡x)3=(−x−x33+O(x5))3=−x3+O(x5)v^3 = (-\tan x)^3 = \left(-x - \frac{x^3}{3} + O(x^5)\right)^3 = -x^3 + O(x^5)

Substitute these into the binomial expansion: (1−tan⁡x)n=1+n(−x−x33)+n(n−1)2(x2+2x43)+n(n−1)(n−2)6(−x3)+O(x4)(1-\tan x)^n = 1 + n\left(-x - \frac{x^3}{3}\right) + \frac{n(n-1)}{2}\left(x^2 + \frac{2x^4}{3}\right) + \frac{n(n-1)(n-2)}{6}(-x^3) + O(x^4) (1−tan⁡x)n=1−nx−n3x3+n(n−1)2x2−n(n−1)(n−2)6x3+O(x4)(1-\tan x)^n = 1 - nx - \frac{n}{3}x^3 + \frac{n(n-1)}{2}x^2 - \frac{n(n-1)(n-2)}{6}x^3 + O(x^4) Rearranging terms by powers of xx: (1−tan⁡x)n=1−nx+n(n−1)2x2+(−n(n−1)(n−2)6−n3)x3+O(x4)(1-\tan x)^n = 1 - nx + \frac{n(n-1)}{2}x^2 + \left(-\frac{n(n-1)(n-2)}{6} - \frac{n}{3}\right)x^3 + O(x^4) (1−tan⁡x)n=1−nx+n(n−1)2x2+−n((n−1)(n−2)+2)6x3+O(x4)(1-\tan x)^n = 1 - nx + \frac{n(n-1)}{2}x^2 + \frac{-n((n-1)(n-2) + 2)}{6}x^3 + O(x^4) (1−tan⁡x)n=1−nx+n(n−1)2x2+−n(n2−3n+2+2)6x3+O(x4)(1-\tan x)^n = 1 - nx + \frac{n(n-1)}{2}x^2 + \frac{-n(n^2-3n+2+2)}{6}x^3 + O(x^4) (1−tan⁡x)n=1−nx+n(n−1)2x2−n(n2−3n+4)6x3+O(x4)(1-\tan x)^n = 1 - nx + \frac{n(n-1)}{2}x^2 - \frac{n(n^2-3n+4)}{6}x^3 + O(x^4) (Equation 2)

Now, add Equation 1 and Equation 2, and subtract 2: Numerator N(x)=(1+sin⁡x)n+(1−tan⁡x)n−2N(x) = (1+\sin x)^n + (1-\tan x)^n - 2 N(x)=(1+nx+n(n−1)2x2+n(n2−3n+1)6x3)+(1−nx+n(n−1)2x2−n(n2−3n+4)6x3)−2+O(x4)N(x) = \left(1 + nx + \frac{n(n-1)}{2}x^2 + \frac{n(n^2-3n+1)}{6}x^3\right) + \left(1 - nx + \frac{n(n-1)}{2}x^2 - \frac{n(n^2-3n+4)}{6}x^3\right) - 2 + O(x^4)

Combine like terms: Constant terms: 1+1−2=01+1-2 = 0 xx terms: nx−nx=0nx - nx = 0 x2x^2 terms: n(n−1)2x2+n(n−1)2x2=n(n−1)x2\frac{n(n-1)}{2}x^2 + \frac{n(n-1)}{2}x^2 = n(n-1)x^2 x3x^3 terms: (n(n2−3n+1)6−n(n2−3n+4)6)x3\left(\frac{n(n^2-3n+1)}{6} - \frac{n(n^2-3n+4)}{6}\right)x^3 =n6(n2−3n+1−(n2−3n+4))x3= \frac{n}{6}(n^2-3n+1 - (n^2-3n+4))x^3 =n6(n2−3n+1−n2+3n−4)x3= \frac{n}{6}(n^2-3n+1 - n^2+3n-4)x^3 =n6(−3)x3=−n2x3= \frac{n}{6}(-3)x^3 = -\frac{n}{2}x^3

So, the numerator is N(x)=n(n−1)x2−n2x3+O(x4)N(x) = n(n-1)x^2 - \frac{n}{2}x^3 + O(x^4).

Now, substitute this back into the limit expression: L=lim⁡x→0n(n−1)x2−n2x3+O(x4)x3L = \lim_{x\to 0}\frac{n(n-1)x^2 - \frac{n}{2}x^3 + O(x^4)}{x^3} L=lim⁡x→0(n(n−1)x−n2+O(x))L = \lim_{x\to 0}\left(\frac{n(n-1)}{x} - \frac{n}{2} + O(x)\right)

Since n=12024n = \frac{1}{2024}, n≠0n \neq 0 and n≠1n \neq 1. Therefore, n(n−1)≠0n(n-1) \neq 0. The term n(n−1)x\frac{n(n-1)}{x} as x→0x \to 0 will tend to ±∞\pm \infty. This means the limit does not exist.

Let's re-examine the problem or my interpretation. The problem might imply that the x2x^2 term cancels out, which is not happening with this direct expansion. This indicates that the question expects a different method or has a specific property.

Let's consider using L'Hopital's rule. Let f(x)=(1+sin⁡x)n+(1−tan⁡x)n−2f(x) = (1+\sin x)^n+(1-\tan x)^n-2. f′(x)=n(1+sin⁡x)n−1cos⁡x+n(1−tan⁡x)n−1(−sec⁡2x)f'(x) = n(1+\sin x)^{n-1}\cos x + n(1-\tan x)^{n-1}(-\sec^2 x) f′(0)=n(1)n−1(1)+n(1)n−1(−1)=n−n=0f'(0) = n(1)^{n-1}(1) + n(1)^{n-1}(-1) = n - n = 0. Denominator derivative: 3x23x^2. So, we have 00\frac{0}{0} form again.

f′′(x)=n(n−1)(1+sin⁡x)n−2cos⁡2x+n(1+sin⁡x)n−1(−sin⁡x)−n(n−1)(1−tan⁡x)n−2(−sec⁡2x)2−n(1−tan⁡x)n−1(2sec⁡x⋅sec⁡xtan⁡x)f''(x) = n(n-1)(1+\sin x)^{n-2}\cos^2 x + n(1+\sin x)^{n-1}(-\sin x) - n(n-1)(1-\tan x)^{n-2}(-\sec^2 x)^2 - n(1-\tan x)^{n-1}(2\sec x \cdot \sec x \tan x) f′′(x)=n(n−1)(1+sin⁡x)n−2cos⁡2x−n(1+sin⁡x)n−1sin⁡x−n(n−1)(1−tan⁡x)n−2sec⁡4x−2n(1−tan⁡x)n−1sec⁡2xtan⁡xf''(x) = n(n-1)(1+\sin x)^{n-2}\cos^2 x - n(1+\sin x)^{n-1}\sin x - n(n-1)(1-\tan x)^{n-2}\sec^4 x - 2n(1-\tan x)^{n-1}\sec^2 x \tan x f′′(0)=n(n−1)(1)n−2(1)2−n(1)n−1(0)−n(n−1)(1)n−2(1)4−2n(1)n−1(1)2(0)f''(0) = n(n-1)(1)^{n-2}(1)^2 - n(1)^{n-1}(0) - n(n-1)(1)^{n-2}(1)^4 - 2n(1)^{n-1}(1)^2(0) f′′(0)=n(n−1)−n(n−1)=0f''(0) = n(n-1) - n(n-1) = 0. Denominator second derivative: 6x6x. So, we have 00\frac{0}{0} form again.

f′′′(x)=ddx(n(n−1)(1+sin⁡x)n−2cos⁡2x−n(1+sin⁡x)n−1sin⁡x−n(n−1)(1−tan⁡x)n−2sec⁡4x−2n(1−tan⁡x)n−1sec⁡2xtan⁡x)f'''(x) = \frac{d}{dx} \left( n(n-1)(1+\sin x)^{n-2}\cos^2 x - n(1+\sin x)^{n-1}\sin x - n(n-1)(1-\tan x)^{n-2}\sec^4 x - 2n(1-\tan x)^{n-1}\sec^2 x \tan x \right) This is going to be very tedious to calculate f′′′(0)f'''(0).

Let's use the Taylor expansion coefficients. We have f(x)=f(0)+f′(0)x+f′′(0)2!x2+f′′′(0)3!x3+O(x4)f(x) = f(0) + f'(0)x + \frac{f''(0)}{2!}x^2 + \frac{f'''(0)}{3!}x^3 + O(x^4). We found f(0)=0f(0)=0, f′(0)=0f'(0)=0, f′′(0)=0f''(0)=0. So, N(x)=f′′′(0)6x3+O(x4)N(x) = \frac{f'''(0)}{6}x^3 + O(x^4). Then the limit would be f′′′(0)6\frac{f'''(0)}{6}.

Let f1(x)=(1+sin⁡x)nf_1(x) = (1+\sin x)^n. f1(0)=1f_1(0)=1. f1′(x)=n(1+sin⁡x)n−1cos⁡x  ⟹  f1′(0)=nf_1'(x) = n(1+\sin x)^{n-1}\cos x \implies f_1'(0)=n. f1′′(x)=n(n−1)(1+sin⁡x)n−2cos⁡2x−n(1+sin⁡x)n−1sin⁡x  ⟹  f1′′(0)=n(n−1)f_1''(x) = n(n-1)(1+\sin x)^{n-2}\cos^2 x - n(1+\sin x)^{n-1}\sin x \implies f_1''(0)=n(n-1). f1′′′(x)=n(n−1)(n−2)(1+sin⁡x)n−3cos⁡3x+n(n−1)(1+sin⁡x)n−2(−2sin⁡xcos⁡x)−n(n−1)(1+sin⁡x)n−2sin⁡xcos⁡x−n(1+sin⁡x)n−1cos⁡xf_1'''(x) = n(n-1)(n-2)(1+\sin x)^{n-3}\cos^3 x + n(n-1)(1+\sin x)^{n-2}(-2\sin x \cos x) - n(n-1)(1+\sin x)^{n-2}\sin x \cos x - n(1+\sin x)^{n-1}\cos x f1′′′(0)=n(n−1)(n−2)(1)3+0−0−n(1)=n(n−1)(n−2)−nf_1'''(0) = n(n-1)(n-2)(1)^3 + 0 - 0 - n(1) = n(n-1)(n-2) - n.

Let f2(x)=(1−tan⁡x)nf_2(x) = (1-\tan x)^n. f2(0)=1f_2(0)=1. f2′(x)=n(1−tan⁡x)n−1(−sec⁡2x)  ⟹  f2′(0)=−nf_2'(x) = n(1-\tan x)^{n-1}(-\sec^2 x) \implies f_2'(0)=-n. f2′′(x)=n(n−1)(1−tan⁡x)n−2(−sec⁡2x)2−n(1−tan⁡x)n−1(2sec⁡x⋅sec⁡xtan⁡x)f_2''(x) = n(n-1)(1-\tan x)^{n-2}(-\sec^2 x)^2 - n(1-\tan x)^{n-1}(2\sec x \cdot \sec x \tan x) f2′′(x)=n(n−1)(1−tan⁡x)n−2sec⁡4x−2n(1−tan⁡x)n−1sec⁡2xtan⁡xf_2''(x) = n(n-1)(1-\tan x)^{n-2}\sec^4 x - 2n(1-\tan x)^{n-1}\sec^2 x \tan x f2′′(0)=n(n−1)(1)4−0=n(n−1)f_2''(0) = n(n-1)(1)^4 - 0 = n(n-1). f2′′′(x)=n(n−1)(n−2)(1−tan⁡x)n−3(−sec⁡2x)3+n(n−1)(1−tan⁡x)n−2(4sec⁡3xtan⁡x)−2n(n−1)(1−tan⁡x)n−2(−sec⁡2x)(sec⁡2xtan⁡x)−2n(1−tan⁡x)n−1(2sec⁡xtan⁡xsec⁡x+sec⁡2xsec⁡2x)f_2'''(x) = n(n-1)(n-2)(1-\tan x)^{n-3}(-\sec^2 x)^3 + n(n-1)(1-\tan x)^{n-2}(4\sec^3 x \tan x) - 2n(n-1)(1-\tan x)^{n-2}(-\sec^2 x)(\sec^2 x \tan x) - 2n(1-\tan x)^{n-1}(2\sec x \tan x \sec x + \sec^2 x \sec^2 x) f2′′′(0)=n(n−1)(n−2)(−1)3+0−0−2n(1)(0+1)=−n(n−1)(n−2)−2nf_2'''(0) = n(n-1)(n-2)(-1)^3 + 0 - 0 - 2n(1)(0+1) = -n(n-1)(n-2) - 2n.

The numerator is N(x)=f1(x)+f2(x)−2N(x) = f_1(x) + f_2(x) - 2. N(0)=f1(0)+f2(0)−2=1+1−2=0N(0) = f_1(0) + f_2(0) - 2 = 1+1-2 = 0. N′(x)=f1′(x)+f2′(x)  ⟹  N′(0)=n+(−n)=0N'(x) = f_1'(x) + f_2'(x) \implies N'(0) = n + (-n) = 0. N′′(x)=f1′′(x)+f2′′(x)  ⟹  N′′(0)=n(n−1)+n(n−1)=2n(n−1)N''(x) = f_1''(x) + f_2''(x) \implies N''(0) = n(n-1) + n(n-1) = 2n(n-1). N′′′(x)=f1′′′(x)+f2′′′(x)  ⟹  N′′′(0)=(n(n−1)(n−2)−n)+(−n(n−1)(n−2)−2n)N'''(x) = f_1'''(x) + f_2'''(x) \implies N'''(0) = (n(n-1)(n-2) - n) + (-n(n-1)(n-2) - 2n). N′′′(0)=n(n−1)(n−2)−n−n(n−1)(n−2)−2n=−3nN'''(0) = n(n-1)(n-2) - n - n(n-1)(n-2) - 2n = -3n.

Now, let's substitute these into the Taylor expansion of the numerator: N(x)=N(0)+N′(0)x+N′′(0)2!x2+N′′′(0)3!x3+O(x4)N(x) = N(0) + N'(0)x + \frac{N''(0)}{2!}x^2 + \frac{N'''(0)}{3!}x^3 + O(x^4) N(x)=0+0⋅x+2n(n−1)2x2+−3n6x3+O(x4)N(x) = 0 + 0 \cdot x + \frac{2n(n-1)}{2}x^2 + \frac{-3n}{6}x^3 + O(x^4) N(x)=n(n−1)x2−n2x3+O(x4)N(x) = n(n-1)x^2 - \frac{n}{2}x^3 + O(x^4).

This result for N(x)N(x) is exactly the same as what I got using direct binomial expansion. This means the x2x^2 term n(n−1)x2n(n-1)x^2 is indeed present and non-zero. If n(n−1)≠0n(n-1) \neq 0, then lim⁡x→0n(n−1)x2−n2x3+O(x4)x3=lim⁡x→0(n(n−1)x−n2+O(x))\lim_{x\to 0}\frac{n(n-1)x^2 - \frac{n}{2}x^3 + O(x^4)}{x^3} = \lim_{x\to 0}\left(\frac{n(n-1)}{x} - \frac{n}{2} + O(x)\right). Since n=12024n = \frac{1}{2024}, n(n−1)=12024(12024−1)=−202320242≠0n(n-1) = \frac{1}{2024}\left(\frac{1}{2024}-1\right) = -\frac{2023}{2024^2} \neq 0. Therefore, the term n(n−1)x\frac{n(n-1)}{x} approaches ∞\infty or −∞-\infty as x→0x \to 0. Specifically, as x→0+x \to 0^+, n(n−1)x→−∞\frac{n(n-1)}{x} \to -\infty. As x→0−x \to 0^-, n(n−1)x→+∞\frac{n(n-1)}{x} \to +\infty. Since the left-hand limit and right-hand limit are not equal, the limit does not exist.

It is possible that the problem is designed to have a zero coefficient for x2x^2. This would happen if n(n−1)=0n(n-1) = 0, which means n=0n=0 or n=1n=1. But n=12024n = \frac{1}{2024}, so this condition is not met.

Let's assume there might be a typo in the question and the denominator should be x2x^2 or the numerator should be different. However, based on the question as written, the limit does not exist. If the question was lim⁡x→0(1+sin⁡x)12024+(1−tan⁡x)12024−2x2\lim_{x\to 0}\frac{(1+\sin x)^{\frac{1}{2024}}+(1-\tan x)^{\frac{1}{2024}}-2}{x^2}, the answer would be n(n−1)n(n-1). If the question was lim⁡x→0(1+sin⁡x)12024−(1−tan⁡x)12024x\lim_{x\to 0}\frac{(1+\sin x)^{\frac{1}{2024}}-(1-\tan x)^{\frac{1}{2024}}}{x}, the answer would be n−(−n)=2nn - (-n) = 2n.

Given the problem as stated, the limit is lim⁡x→0(n(n−1)x−n2)\lim_{x\to 0}\left(\frac{n(n-1)}{x} - \frac{n}{2}\right). This limit does not exist.

Final check of all steps. The Taylor series expansions and their combination seem robust. L'Hopital's rule confirmed the same coefficients. The only way the limit could be a finite value is if n(n−1)=0n(n-1)=0, which implies n=0n=0 or n=1n=1. However, n=1/2024n=1/2024. Thus, the limit does not exist.

However, in JEE/NEET context, if a multiple choice question is given, usually there is a finite answer. Let's consider if there's any implicit assumption. Could it be that the question expects some cancellation of terms for some specific value of n? No, n=1/2024n=1/2024 is a fixed value.

Perhaps the question implicitly assumes a different kind of function or a misprint. If the question was lim⁡x→0(1+sin⁡x)12024+(1−sin⁡x)12024−2x3\lim_{x\to 0}\frac{(1+\sin x)^{\frac{1}{2024}}+(1-\sin x)^{\frac{1}{2024}}-2}{x^3} Then for (1−sin⁡x)n(1-\sin x)^n: 1−nsin⁡x+n(n−1)2(sin⁡x)2−n(n−1)(n−2)6(sin⁡x)3+O(x4)1 - n\sin x + \frac{n(n-1)}{2}(\sin x)^2 - \frac{n(n-1)(n-2)}{6}(\sin x)^3 + O(x^4) =1−n(x−x3/6)+n(n−1)2(x2−x4/3)−n(n−1)(n−2)6(x3)+O(x4)= 1 - n(x - x^3/6) + \frac{n(n-1)}{2}(x^2 - x^4/3) - \frac{n(n-1)(n-2)}{6}(x^3) + O(x^4) =1−nx+nx36+n(n−1)2x2−n(n−1)(n−2)6x3+O(x4)= 1 - nx + n\frac{x^3}{6} + \frac{n(n-1)}{2}x^2 - \frac{n(n-1)(n-2)}{6}x^3 + O(x^4) Adding this to (1+sin⁡x)n(1+\sin x)^n: (1+sin⁡x)n+(1−sin⁡x)n−2(1+\sin x)^n + (1-\sin x)^n - 2 =(1+nx+n(n−1)2x2+n(n2−3n+1)6x3)+(1−nx+n(n−1)2x2−n(n2−3n+1)6x3)−2+O(x4)= (1 + nx + \frac{n(n-1)}{2}x^2 + \frac{n(n^2-3n+1)}{6}x^3) + (1 - nx + \frac{n(n-1)}{2}x^2 - \frac{n(n^2-3n+1)}{6}x^3) - 2 + O(x^4) =2+n(n−1)x2−2+O(x4)= 2 + n(n-1)x^2 - 2 + O(x^4) =n(n−1)x2+O(x4)= n(n-1)x^2 + O(x^4). In this case, the limit would be lim⁡x→0n(n−1)x2+O(x4)x3=lim⁡x→0(n(n−1)x+O(x))\lim_{x\to 0}\frac{n(n-1)x^2 + O(x^4)}{x^3} = \lim_{x\to 0}\left(\frac{n(n-1)}{x} + O(x)\right), which still does not exist.

The only scenario where the limit exists and is finite is if the x2x^2 term in the numerator vanishes, i.e., n(n−1)=0n(n-1)=0. This would mean n=0n=0 or n=1n=1. But n=1/2024n = 1/2024.

Therefore, based on the provided question, the limit does not exist.