Question
Question: $\lim_{x\to 0} \frac{sin(\pi cos^2x)}{x^2}$...
limx→0x2sin(πcos2x)
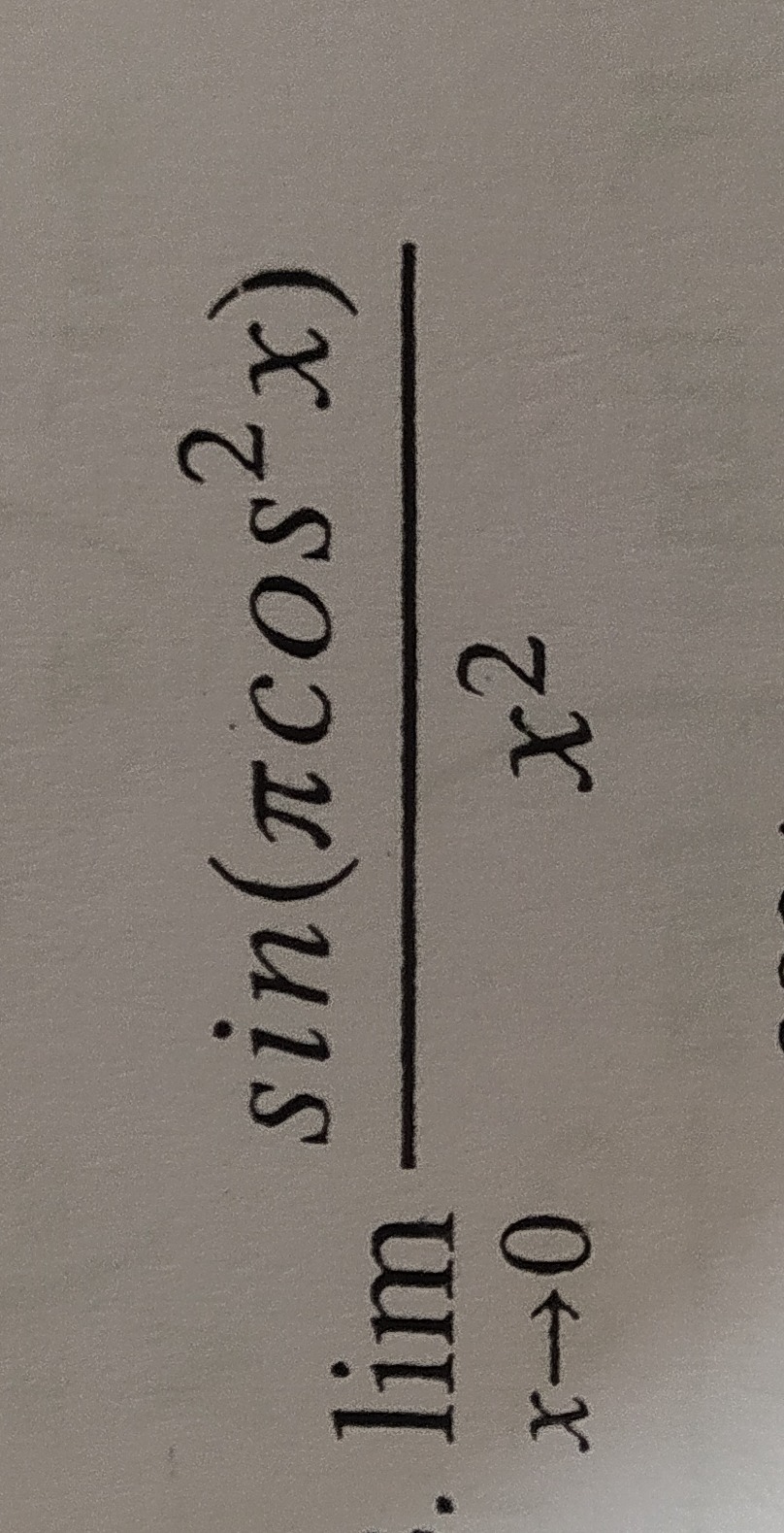
Answer
π
Explanation
Solution
The limit is of the form 00.
Use the identity cos2x=1−sin2x in the argument of sine: πcos2x=π(1−sin2x)=π−πsin2x.
Use the identity sin(π−θ)=sinθ to get sin(πcos2x)=sin(π−πsin2x)=sin(πsin2x).
The limit becomes limx→0x2sin(πsin2x).
Rewrite the expression as πsin2xsin(πsin2x)⋅x2πsin2x.
Take the limit of each part separately.
limx→0πsin2xsin(πsin2x)=1 using the standard limit limy→0ysiny=1 with y=πsin2x.
limx→0x2πsin2x=πlimx→0(xsinx)2=π(1)2=π using the standard limit limx→0xsinx=1.
The overall limit is the product of the two limits: 1⋅π=π.
