Question

$\lim_{x\to 0} \frac{e^{\frac{1}{x}}-1}{e^{\frac{1}{x}}+1}$

Answer 1

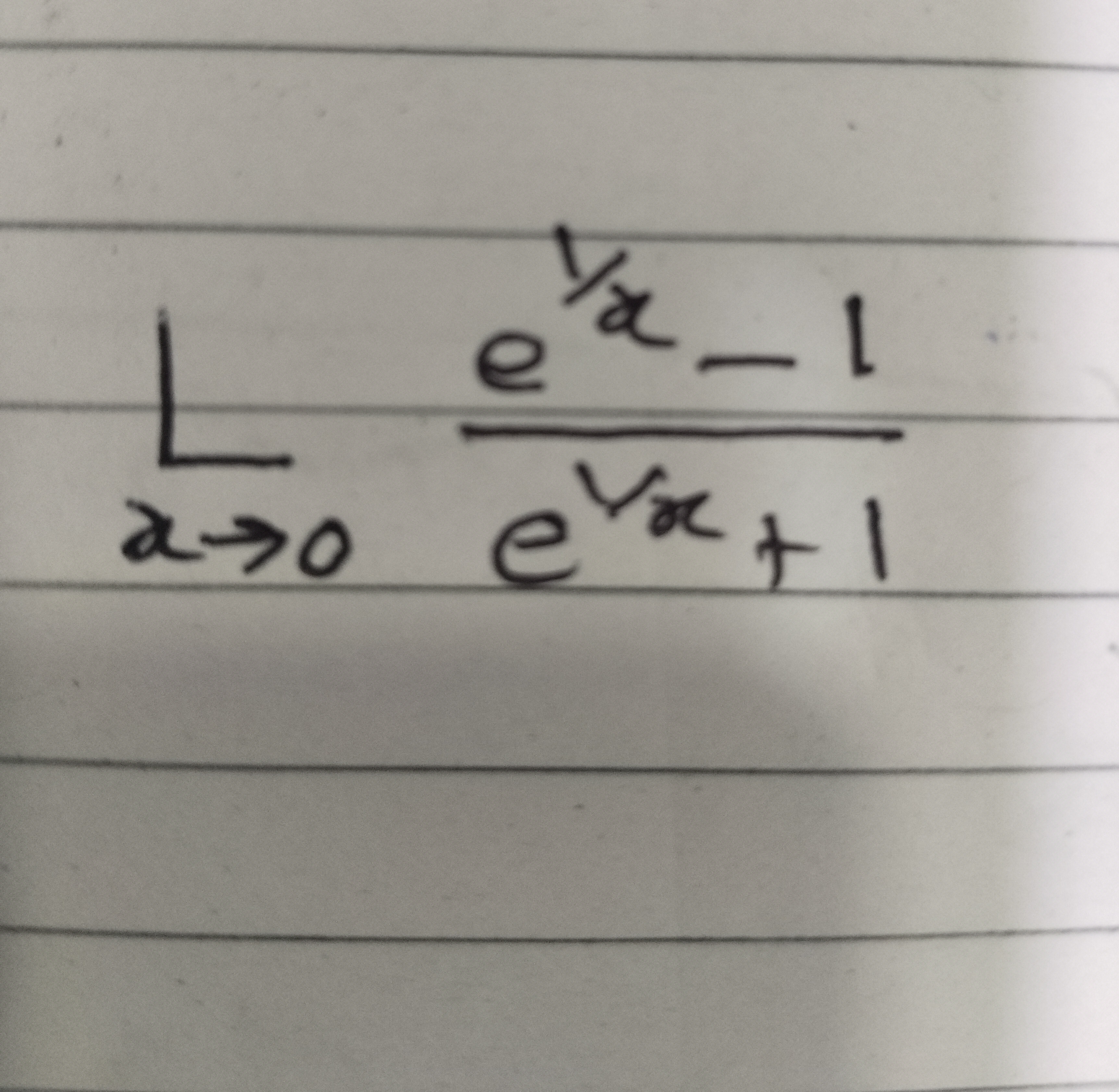
Does not exist

Answer 2

To evaluate the limit $\lim_{x\to 0} \frac{e^{\frac{1}{x}}-1}{e^{\frac{1}{x}}+1}$, we need to consider the left-hand limit (LHL) and the right-hand limit (RHL) separately, as the behavior of $\frac{1}{x}$ changes significantly as $x$ approaches $0$ from the positive and negative sides.

1. Right-Hand Limit (RHL):

As $x \to 0^+$, we have $\frac{1}{x} \to +\infty$.
Therefore, $e^{\frac{1}{x}} \to +\infty$.
The limit becomes: $\lim_{x\to 0^+} \frac{e^{\frac{1}{x}}-1}{e^{\frac{1}{x}}+1}$ To evaluate this, divide the numerator and denominator by $e^{\frac{1}{x}}$: $\lim_{x\to 0^+} \frac{\frac{e^{\frac{1}{x}}}{e^{\frac{1}{x}}}-\frac{1}{e^{\frac{1}{x}}}}{\frac{e^{\frac{1}{x}}}{e^{\frac{1}{x}}}+\frac{1}{e^{\frac{1}{x}}}} = \lim_{x\to 0^+} \frac{1-e^{-\frac{1}{x}}}{1+e^{-\frac{1}{x}}}$ As $x \to 0^+$, $\frac{1}{x} \to +\infty$, so $-\frac{1}{x} \to -\infty$.
Thus, $e^{-\frac{1}{x}} \to 0$.
Substituting this value: $\frac{1-0}{1+0} = 1$ So, the RHL is $1$.

2. Left-Hand Limit (LHL):

As $x \to 0^-$, we have $\frac{1}{x} \to -\infty$.
Therefore, $e^{\frac{1}{x}} \to 0$.
The limit becomes: $\lim_{x\to 0^-} \frac{e^{\frac{1}{x}}-1}{e^{\frac{1}{x}}+1}$ Substitute $e^{\frac{1}{x}} = 0$ into the expression: $\frac{0-1}{0+1} = \frac{-1}{1} = -1$ So, the LHL is $-1$.

Since the left-hand limit ($-1$) is not equal to the right-hand limit ($1$), the limit of the function as $x \to 0$ does not exist.