Solveeit Logo
Login

Question

Question: $\lim_{x\to 0} \frac{(1+\sin x)^{\frac{1}{2014}}+(1-\tan x)^{\frac{1}{2014}}-2}{x^{3}}$...

lim⁡x→0(1+sin⁡x)12014+(1−tan⁡x)12014−2x3\lim_{x\to 0} \frac{(1+\sin x)^{\frac{1}{2014}}+(1-\tan x)^{\frac{1}{2014}}-2}{x^{3}}

Answer

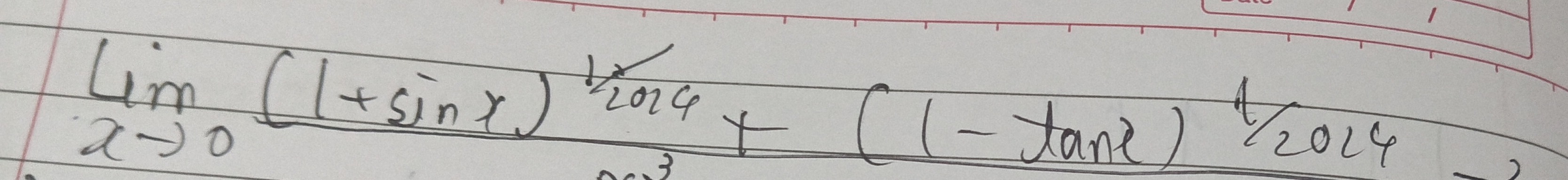
Does not exist

Explanation

Solution

To evaluate the limit lim⁡x→0(1+sin⁡x)12014+(1−tan⁡x)12014−2x3\lim_{x\to 0} \frac{(1+\sin x)^{\frac{1}{2014}}+(1-\tan x)^{\frac{1}{2014}}-2}{x^{3}}, we will use the Taylor series expansions for sin⁡x\sin x, tan⁡x\tan x, and the generalized binomial theorem.

Let n=12014n = \frac{1}{2014}. The generalized binomial expansion for (1+u)n(1+u)^n around u=0u=0 is: (1+u)n=1+nu+n(n−1)2!u2+n(n−1)(n−2)3!u3+O(u4)(1+u)^n = 1 + nu + \frac{n(n-1)}{2!}u^2 + \frac{n(n-1)(n-2)}{3!}u^3 + O(u^4).

We need the Taylor series expansions for sin⁡x\sin x and tan⁡x\tan x around x=0x=0 up to the x3x^3 term: sin⁡x=x−x36+O(x5)\sin x = x - \frac{x^3}{6} + O(x^5) tan⁡x=x+x33+O(x5)\tan x = x + \frac{x^3}{3} + O(x^5)

1. Expand (1+sin⁡x)n(1+\sin x)^n: Let u=sin⁡xu = \sin x. u=x−x36+O(x5)u = x - \frac{x^3}{6} + O(x^5) u2=(sin⁡x)2=(x−x36+O(x5))2=x2−x43+O(x6)u^2 = (\sin x)^2 = \left(x - \frac{x^3}{6} + O(x^5)\right)^2 = x^2 - \frac{x^4}{3} + O(x^6) u3=(sin⁡x)3=(x−x36+O(x5))3=x3+O(x5)u^3 = (\sin x)^3 = \left(x - \frac{x^3}{6} + O(x^5)\right)^3 = x^3 + O(x^5)

Substitute these into the binomial expansion for (1+sin⁡x)n(1+\sin x)^n: (1+sin⁡x)n=1+n(x−x36)+n(n−1)2(x2−x43)+n(n−1)(n−2)6(x3)+O(x4)(1+\sin x)^n = 1 + n\left(x - \frac{x^3}{6}\right) + \frac{n(n-1)}{2}\left(x^2 - \frac{x^4}{3}\right) + \frac{n(n-1)(n-2)}{6}(x^3) + O(x^4) Collecting terms by powers of xx: (1+sin⁡x)n=1+nx+n(n−1)2x2+(n(n−1)(n−2)6−n6)x3+O(x4)(1+\sin x)^n = 1 + nx + \frac{n(n-1)}{2}x^2 + \left(\frac{n(n-1)(n-2)}{6} - \frac{n}{6}\right)x^3 + O(x^4) (1+sin⁡x)n=1+nx+n(n−1)2x2+n(n2−3n+1)6x3+O(x4)(1+\sin x)^n = 1 + nx + \frac{n(n-1)}{2}x^2 + \frac{n(n^2-3n+1)}{6}x^3 + O(x^4) (Equation 1)

2. Expand (1−tan⁡x)n(1-\tan x)^n: Let v=−tan⁡xv = -\tan x. v=−(x+x33+O(x5))=−x−x33+O(x5)v = -\left(x + \frac{x^3}{3} + O(x^5)\right) = -x - \frac{x^3}{3} + O(x^5) v2=(−tan⁡x)2=(−x−x33+O(x5))2=x2+2x43+O(x6)v^2 = (-\tan x)^2 = \left(-x - \frac{x^3}{3} + O(x^5)\right)^2 = x^2 + \frac{2x^4}{3} + O(x^6) v3=(−tan⁡x)3=(−x−x33+O(x5))3=−x3+O(x5)v^3 = (-\tan x)^3 = \left(-x - \frac{x^3}{3} + O(x^5)\right)^3 = -x^3 + O(x^5)

Substitute these into the binomial expansion for (1−tan⁡x)n(1-\tan x)^n: (1−tan⁡x)n=1+n(−x−x33)+n(n−1)2(x2+2x43)+n(n−1)(n−2)6(−x3)+O(x4)(1-\tan x)^n = 1 + n\left(-x - \frac{x^3}{3}\right) + \frac{n(n-1)}{2}\left(x^2 + \frac{2x^4}{3}\right) + \frac{n(n-1)(n-2)}{6}(-x^3) + O(x^4) Collecting terms by powers of xx: (1−tan⁡x)n=1−nx+n(n−1)2x2+(−n(n−1)(n−2)6−n3)x3+O(x4)(1-\tan x)^n = 1 - nx + \frac{n(n-1)}{2}x^2 + \left(-\frac{n(n-1)(n-2)}{6} - \frac{n}{3}\right)x^3 + O(x^4) (1−tan⁡x)n=1−nx+n(n−1)2x2−n(n2−3n+4)6x3+O(x4)(1-\tan x)^n = 1 - nx + \frac{n(n-1)}{2}x^2 - \frac{n(n^2-3n+4)}{6}x^3 + O(x^4) (Equation 2)

3. Combine the expansions for the numerator: Let N(x)=(1+sin⁡x)n+(1−tan⁡x)n−2N(x) = (1+\sin x)^n + (1-\tan x)^n - 2. Add Equation 1 and Equation 2, then subtract 2: N(x)=(1+nx+n(n−1)2x2+n(n2−3n+1)6x3)+(1−nx+n(n−1)2x2−n(n2−3n+4)6x3)−2+O(x4)N(x) = \left(1 + nx + \frac{n(n-1)}{2}x^2 + \frac{n(n^2-3n+1)}{6}x^3\right) + \left(1 - nx + \frac{n(n-1)}{2}x^2 - \frac{n(n^2-3n+4)}{6}x^3\right) - 2 + O(x^4)

Combine like terms: Constant terms: 1+1−2=01+1-2 = 0 xx terms: nx−nx=0nx - nx = 0 x2x^2 terms: n(n−1)2x2+n(n−1)2x2=n(n−1)x2\frac{n(n-1)}{2}x^2 + \frac{n(n-1)}{2}x^2 = n(n-1)x^2 x3x^3 terms: (n(n2−3n+1)6−n(n2−3n+4)6)x3=n6(n2−3n+1−(n2−3n+4))x3=n6(−3)x3=−n2x3\left(\frac{n(n^2-3n+1)}{6} - \frac{n(n^2-3n+4)}{6}\right)x^3 = \frac{n}{6}(n^2-3n+1 - (n^2-3n+4))x^3 = \frac{n}{6}(-3)x^3 = -\frac{n}{2}x^3

So, the numerator is N(x)=n(n−1)x2−n2x3+O(x4)N(x) = n(n-1)x^2 - \frac{n}{2}x^3 + O(x^4).

4. Evaluate the limit: The limit expression becomes: L=lim⁡x→0n(n−1)x2−n2x3+O(x4)x3L = \lim_{x\to 0}\frac{n(n-1)x^2 - \frac{n}{2}x^3 + O(x^4)}{x^3} Divide each term in the numerator by x3x^3: L=lim⁡x→0(n(n−1)x−n2+O(x))L = \lim_{x\to 0}\left(\frac{n(n-1)}{x} - \frac{n}{2} + O(x)\right)

Given n=12014n = \frac{1}{2014}. Therefore, n(n−1)=12014(12014−1)=12014(−20132014)=−201320142n(n-1) = \frac{1}{2014}\left(\frac{1}{2014}-1\right) = \frac{1}{2014}\left(-\frac{2013}{2014}\right) = -\frac{2013}{2014^2}. This value is a non-zero constant.

As x→0x \to 0, the term n(n−1)x\frac{n(n-1)}{x} approaches ±∞\pm \infty. Specifically: As x→0+x \to 0^+, n(n−1)x=−201320142x→−∞\frac{n(n-1)}{x} = \frac{-\frac{2013}{2014^2}}{x} \to -\infty. As x→0−x \to 0^-, n(n−1)x=−201320142x→+∞\frac{n(n-1)}{x} = \frac{-\frac{2013}{2014^2}}{x} \to +\infty.

Since the left-hand limit and the right-hand limit are not equal, the limit does not exist.

The final answer is Does not exist\boxed{\text{Does not exist}}.

Explanation of the solution: The numerator is expanded using Taylor series for (1+sin⁡x)n(1+\sin x)^n and (1−tan⁡x)n(1-\tan x)^n up to x3x^3 terms. (1+sin⁡x)n=1+nx+n(n−1)2x2+n(n2−3n+1)6x3+O(x4)(1+\sin x)^n = 1 + nx + \frac{n(n-1)}{2}x^2 + \frac{n(n^2-3n+1)}{6}x^3 + O(x^4) (1−tan⁡x)n=1−nx+n(n−1)2x2−n(n2−3n+4)6x3+O(x4)(1-\tan x)^n = 1 - nx + \frac{n(n-1)}{2}x^2 - \frac{n(n^2-3n+4)}{6}x^3 + O(x^4) Adding these and subtracting 2, the numerator becomes n(n−1)x2−n2x3+O(x4)n(n-1)x^2 - \frac{n}{2}x^3 + O(x^4). The limit is lim⁡x→0n(n−1)x2−n2x3+O(x4)x3=lim⁡x→0(n(n−1)x−n2+O(x))\lim_{x\to 0}\frac{n(n-1)x^2 - \frac{n}{2}x^3 + O(x^4)}{x^3} = \lim_{x\to 0}\left(\frac{n(n-1)}{x} - \frac{n}{2} + O(x)\right). Since n=12014n = \frac{1}{2014}, n(n−1)≠0n(n-1) \neq 0. The term n(n−1)x\frac{n(n-1)}{x} approaches ±∞\pm \infty as x→0x \to 0, causing the limit to not exist.