Question

$\lim_{x \to \infty} (\sqrt{x^2-x+1} - ax + 2b) = 0$, then a = ------.

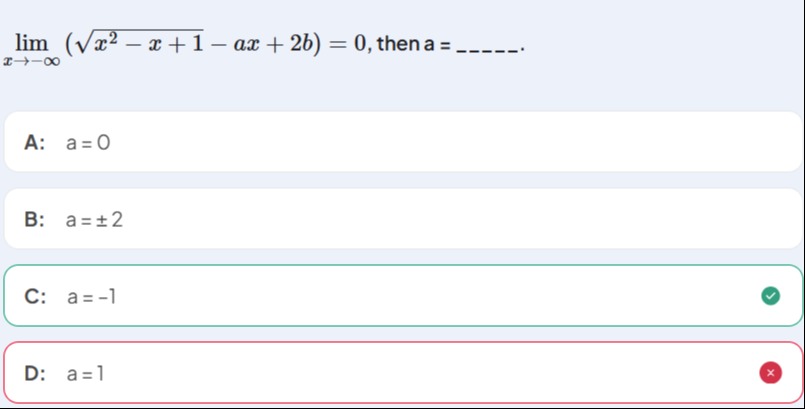
• A. a = 0
• B. a = ±2
• C. a = -1
• D. a = 1

Answer 1

Answer: (D)

a = 1

Answer 2

We have

$$\lim_{x\to\infty}\left(\sqrt{x^2-x+1}-ax+2b\right)=0.$$

For large $x$, write

$$\sqrt{x^2-x+1}=x\sqrt{1-\frac{1}{x}+\frac{1}{x^2}}.$$

Using the expansion $\sqrt{1+u}\approx1+\frac{u}{2}$ for small $u$ (where $u=-\frac{1}{x}+\frac{1}{x^2}$), we get:

$$\sqrt{1-\frac{1}{x}+\frac{1}{x^2}}\approx 1-\frac{1}{2x}\quad (\text{ignoring higher order terms}),$$

so that

$$\sqrt{x^2-x+1}\approx x-\frac{1}{2}.$$

Therefore,

$$\sqrt{x^2-x+1}-ax+2b \approx (1-a)x-\frac{1}{2}+2b.$$

For the limit to be 0 as $x\to \infty$, the coefficient of $x$ must vanish:

$$1-a=0 \quad\implies\quad a=1.$$

In summary: Expand $\sqrt{x^2-x+1}$ for large $x$ to get $x-\frac{1}{2}$. Equate the coefficient of $x$ to zero in $(x-\frac{1}{2})-ax+2b$ to obtain $1-a=0$ so $a=1$.