Solveeit Logo
Login

Question

Question: $\lim_{x \to \infty} \sqrt{x} \left( \sqrt{x + \sqrt{x + \sqrt{x + \sqrt{x}}}} - \sqrt{x + \sqrt{x}}...

lim⁡x→∞x(x+x+x+x−x+x)\lim_{x \to \infty} \sqrt{x} \left( \sqrt{x + \sqrt{x + \sqrt{x + \sqrt{x}}}} - \sqrt{x + \sqrt{x}} \right) is equal to

A

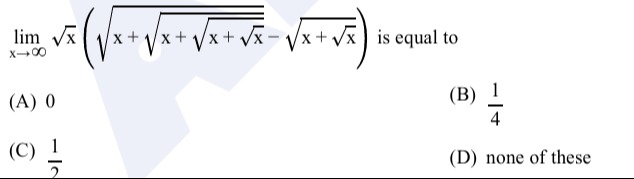
0

B

14\frac{1}{4}

C

12\frac{1}{2}

D

none of these

Answer

1/4

Explanation

Solution

Let the given limit be LL.

L=lim⁡x→∞x(x+x+x+x−x+x)L = \lim_{x \to \infty} \sqrt{x} \left( \sqrt{x + \sqrt{x + \sqrt{x + \sqrt{x}}}} - \sqrt{x + \sqrt{x}} \right)

This is an indeterminate form of type ∞×(∞−∞)\infty \times (\infty - \infty). We will use the rationalization technique.

Let A=x+x+x+xA = \sqrt{x + \sqrt{x + \sqrt{x + \sqrt{x}}}} and B=x+xB = \sqrt{x + \sqrt{x}}.

The expression inside the parenthesis is A−BA - B. We multiply and divide by (A+B)(A + B):

L=lim⁡x→∞x(A−B)(A+B)A+B=lim⁡x→∞xA2−B2A+BL = \lim_{x \to \infty} \sqrt{x} \frac{(A - B)(A + B)}{A + B} = \lim_{x \to \infty} \sqrt{x} \frac{A^2 - B^2}{A + B}

Calculate A2−B2A^2 - B^2:

A2=x+x+x+xA^2 = x + \sqrt{x + \sqrt{x + \sqrt{x}}}

B2=x+xB^2 = x + \sqrt{x}

A2−B2=(x+x+x+x)−(x+x)A^2 - B^2 = (x + \sqrt{x + \sqrt{x + \sqrt{x}}}) - (x + \sqrt{x})

A2−B2=x+x+x−xA^2 - B^2 = \sqrt{x + \sqrt{x + \sqrt{x}}} - \sqrt{x}

Substitute this back into the limit expression:

L=lim⁡x→∞xx+x+x−xx+x+x+x+x+xL = \lim_{x \to \infty} \sqrt{x} \frac{\sqrt{x + \sqrt{x + \sqrt{x}}} - \sqrt{x}}{\sqrt{x + \sqrt{x + \sqrt{x + \sqrt{x}}}} + \sqrt{x + \sqrt{x}}}

The numerator is still an indeterminate form (∞−∞)(\infty - \infty). Let C=x+x+xC = \sqrt{x + \sqrt{x + \sqrt{x}}} and D=xD = \sqrt{x}.

We rationalize the numerator by multiplying and dividing by (C+D)(C + D):

C−D=(C−D)(C+D)C+D=C2−D2C+DC - D = \frac{(C - D)(C + D)}{C + D} = \frac{C^2 - D^2}{C + D}

C2=x+x+xC^2 = x + \sqrt{x + \sqrt{x}}

D2=xD^2 = x

C2−D2=(x+x+x)−x=x+xC^2 - D^2 = (x + \sqrt{x + \sqrt{x}}) - x = \sqrt{x + \sqrt{x}}

Now substitute this back into the expression for LL:

L=lim⁡x→∞xx+x(x+x+x+x+x+x)(x+x+x+x)L = \lim_{x \to \infty} \sqrt{x} \frac{\sqrt{x + \sqrt{x}}}{\left( \sqrt{x + \sqrt{x + \sqrt{x + \sqrt{x}}}} + \sqrt{x + \sqrt{x}} \right) \left( \sqrt{x + \sqrt{x + \sqrt{x}}} + \sqrt{x} \right)}

Now, we extract x\sqrt{x} from each term in the denominator and the numerator.

Numerator: xx+x=xx(1+1/x)=x⋅x1+1/x=x1+1/x\sqrt{x} \sqrt{x + \sqrt{x}} = \sqrt{x} \sqrt{x(1 + 1/\sqrt{x})} = \sqrt{x} \cdot \sqrt{x} \sqrt{1 + 1/\sqrt{x}} = x \sqrt{1 + 1/\sqrt{x}}

Denominator terms:

  1. x+x+x+x=x(1+1x1+1x1+1x)=x1+1x1+1x1+1x\sqrt{x + \sqrt{x + \sqrt{x + \sqrt{x}}}} = \sqrt{x \left(1 + \frac{1}{\sqrt{x}} \sqrt{1 + \frac{1}{\sqrt{x}} \sqrt{1 + \frac{1}{\sqrt{x}}}}\right)} = \sqrt{x} \sqrt{1 + \frac{1}{\sqrt{x}} \sqrt{1 + \frac{1}{\sqrt{x}} \sqrt{1 + \frac{1}{\sqrt{x}}}}}
  2. x+x=x(1+1x)=x1+1x\sqrt{x + \sqrt{x}} = \sqrt{x \left(1 + \frac{1}{\sqrt{x}}\right)} = \sqrt{x} \sqrt{1 + \frac{1}{\sqrt{x}}}
  3. x+x+x=x(1+1x1+1x)=x1+1x1+1x\sqrt{x + \sqrt{x + \sqrt{x}}} = \sqrt{x \left(1 + \frac{1}{\sqrt{x}} \sqrt{1 + \frac{1}{\sqrt{x}}}\right)} = \sqrt{x} \sqrt{1 + \frac{1}{\sqrt{x}} \sqrt{1 + \frac{1}{\sqrt{x}}}}
  4. x=x\sqrt{x} = \sqrt{x}

Substitute these into the expression for LL:

L=lim⁡x→∞x1+1/x(x1+1x1+1x1+1x+x1+1x)(x1+1x1+1x+x)L = \lim_{x \to \infty} \frac{x \sqrt{1 + 1/\sqrt{x}}}{\left( \sqrt{x} \sqrt{1 + \frac{1}{\sqrt{x}} \sqrt{1 + \frac{1}{\sqrt{x}} \sqrt{1 + \frac{1}{\sqrt{x}}}}} + \sqrt{x} \sqrt{1 + \frac{1}{\sqrt{x}}} \right) \left( \sqrt{x} \sqrt{1 + \frac{1}{\sqrt{x}} \sqrt{1 + \frac{1}{\sqrt{x}}}} + \sqrt{x} \right)}

Factor out x\sqrt{x} from each parenthesis in the denominator:

L=lim⁡x→∞x1+1/xx(1+1x1+1x1+1x+1+1x)(1+1x1+1x+1)L = \lim_{x \to \infty} \frac{x \sqrt{1 + 1/\sqrt{x}}}{x \left( \sqrt{1 + \frac{1}{\sqrt{x}} \sqrt{1 + \frac{1}{\sqrt{x}} \sqrt{1 + \frac{1}{\sqrt{x}}}}} + \sqrt{1 + \frac{1}{\sqrt{x}}} \right) \left( \sqrt{1 + \frac{1}{\sqrt{x}} \sqrt{1 + \frac{1}{\sqrt{x}}}} + 1 \right)}

Cancel out xx from numerator and denominator:

L=lim⁡x→∞1+1/x(1+1x1+1x1+1x+1+1x)(1+1x1+1x+1)L = \lim_{x \to \infty} \frac{\sqrt{1 + 1/\sqrt{x}}}{\left( \sqrt{1 + \frac{1}{\sqrt{x}} \sqrt{1 + \frac{1}{\sqrt{x}} \sqrt{1 + \frac{1}{\sqrt{x}}}}} + \sqrt{1 + \frac{1}{\sqrt{x}}} \right) \left( \sqrt{1 + \frac{1}{\sqrt{x}} \sqrt{1 + \frac{1}{\sqrt{x}}}} + 1 \right)}

As x→∞x \to \infty, terms like 1/x1/\sqrt{x} tend to 00.

Let's evaluate each part:

Numerator: 1+0=1\sqrt{1 + 0} = 1

First parenthesis in denominator:

1+0⋅1+0⋅1+0+1+0=1+1=1+1=2\sqrt{1 + 0 \cdot \sqrt{1 + 0 \cdot \sqrt{1 + 0}}} + \sqrt{1 + 0} = \sqrt{1} + \sqrt{1} = 1 + 1 = 2

Second parenthesis in denominator:

1+0⋅1+0+1=1+1=1+1=2\sqrt{1 + 0 \cdot \sqrt{1 + 0}} + 1 = \sqrt{1} + 1 = 1 + 1 = 2

So, the limit becomes:

L=1(2)(2)=14L = \frac{1}{(2)(2)} = \frac{1}{4}

The final answer is 14\boxed{\frac{1}{4}}.