Question
Question: $\lim_{x \to \infty} \frac{lnx}{x}$...
limx→∞xlnx
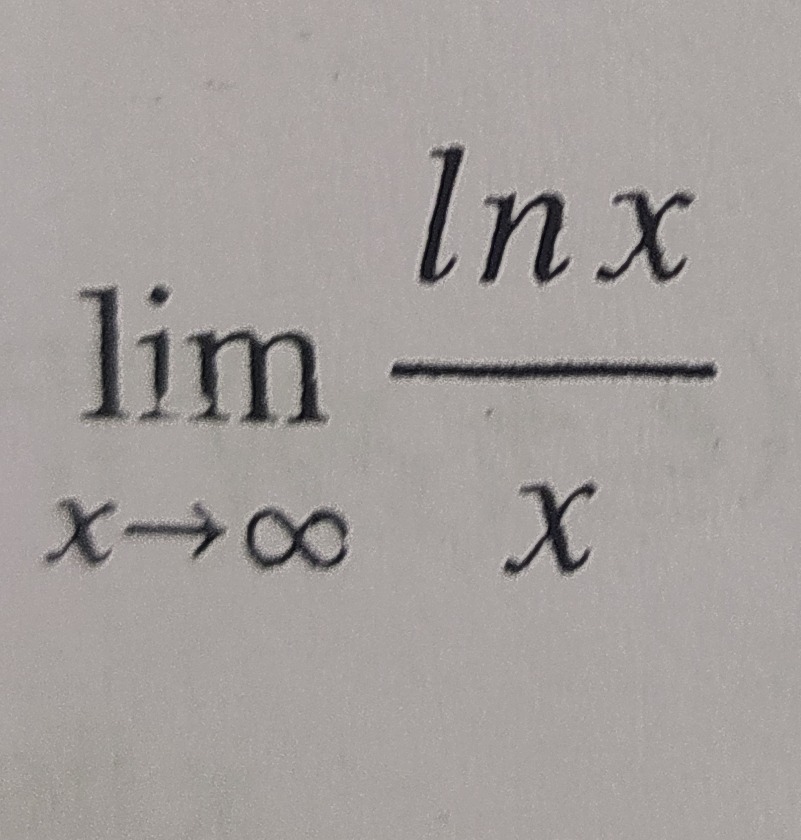
Answer
0
Explanation
Solution
The limit is of the form ∞∞. Apply L'Hôpital's Rule. Differentiate the numerator (lnx) to get 1/x. Differentiate the denominator (x) to get 1. The new limit is limx→∞11/x=limx→∞x1=0.
