Question
Question: $\lim_{x \to \infty} \frac{\int_{0}^{x^2} sin t^5 dt}{x^{12}}$...
limx→∞x12∫0x2sint5dt
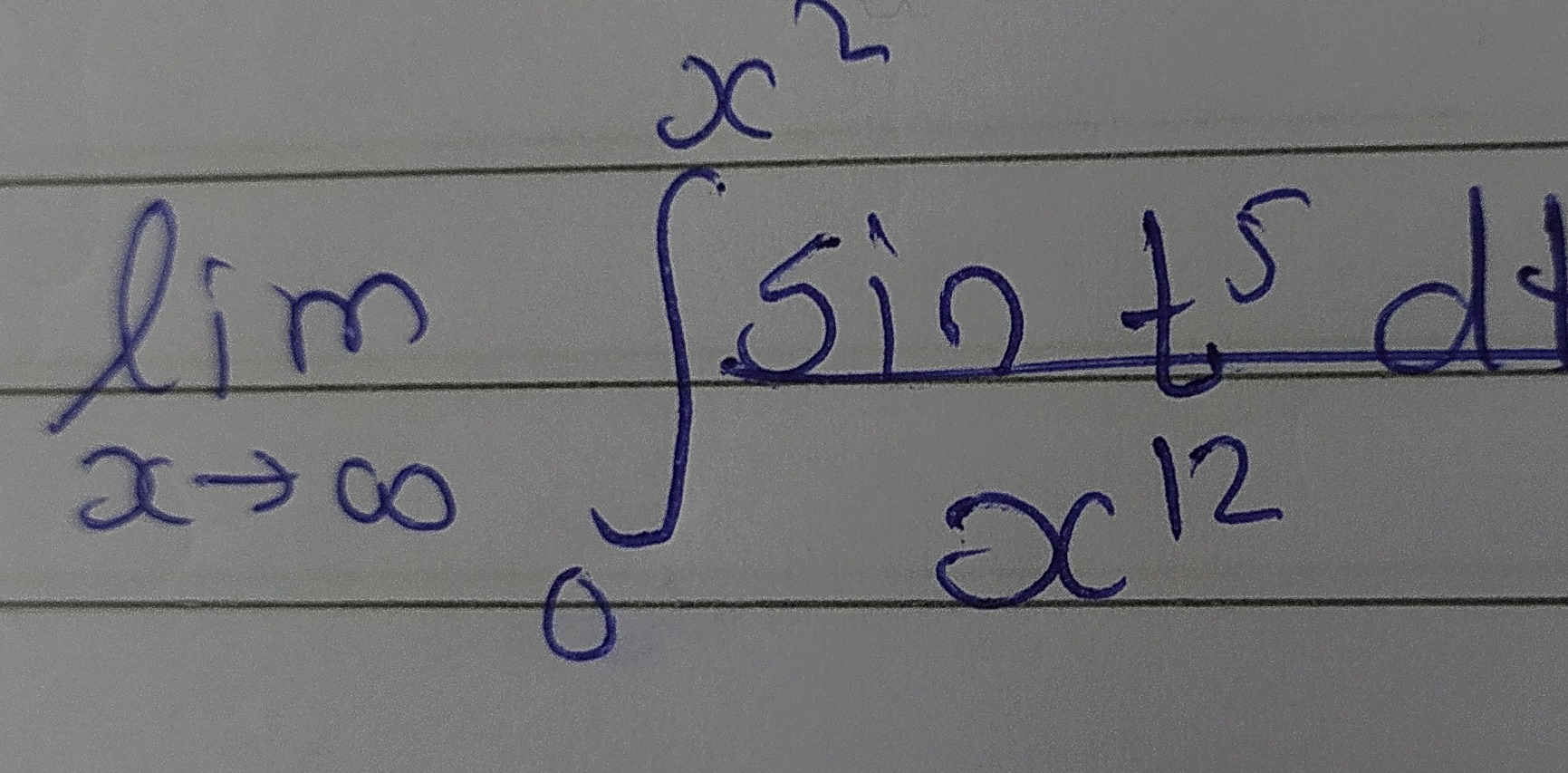
0
Solution
To evaluate the limit limx→∞x12∫0x2sint5dt, we first analyze the form of the limit as x→∞.
Let N(x)=∫0x2sint5dt and D(x)=x12.
As x→∞, the denominator D(x)=x12→∞.
For the numerator N(x)=∫0x2sint5dt: As x→∞, the upper limit x2→∞. The integral ∫0∞sint5dt is a type of Fresnel integral. To check its convergence, we can use the substitution u=t5, so t=u1/5 and dt=51u−4/5du. The integral becomes ∫0∞sinu⋅51u−4/5du=51∫0∞u4/5sinudu. This integral converges by Dirichlet's test, as u4/51 is monotonically decreasing and tends to 0 as u→∞, and ∫sinudu is bounded. Therefore, limx→∞∫0x2sint5dt converges to a finite value.
Since the numerator approaches a finite value and the denominator approaches infinity, the limit is of the form ∞finite value, which is 0.
Alternatively, if we assume the limit is of the indeterminate form ∞∞ (which is a common assumption for such problems in competitive exams, leading to the application of L'Hopital's rule even if not strictly applicable by definition), we can apply L'Hopital's rule.
Let f(x)=∫0x2sint5dt and g(x)=x12. We need to find f′(x) and g′(x).
Using the Leibniz integral rule, dxd∫a(x)b(x)h(t)dt=h(b(x))b′(x)−h(a(x))a′(x): f′(x)=dxd∫0x2sint5dt=sin((x2)5)⋅dxd(x2)−sin(05)⋅dxd(0) f′(x)=sin(x10)⋅(2x)−0 f′(x)=2xsin(x10)
Now, find the derivative of the denominator: g′(x)=dxd(x12)=12x11
Applying L'Hopital's rule: limx→∞g(x)f(x)=limx→∞g′(x)f′(x) =limx→∞12x112xsin(x10) =limx→∞6x10sin(x10)
Let y=x10. As x→∞, y→∞. The limit becomes: limy→∞6ysiny
We know that the sine function is bounded, i.e., −1≤siny≤1. Dividing by 6y (which is positive for y→∞): 6y−1≤6ysiny≤6y1
As y→∞, 6y−1→0 and 6y1→0. By the Squeeze Theorem, limy→∞6ysiny=0.
Both methods yield the same result.
