Question
Question: $\lim_{x \to \frac{\pi}{4}}(\cos x - \sin x)^{(x-\frac{\pi}{4})}$ is equal to :...
limx→4π(cosx−sinx)(x−4π) is equal to :
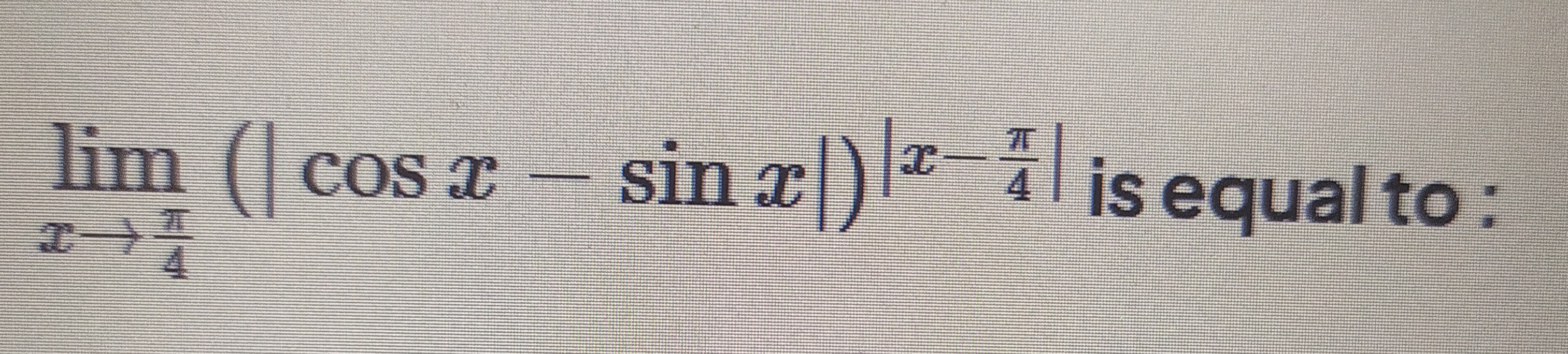
1
Solution
To evaluate the limit limx→4π(cosx−sinx)(x−4π), first determine its form.
As x→4π:
The base cosx−sinx→cos(4π)−sin(4π)=21−21=0.
The exponent x−4π→4π−4π=0.
So, the limit is of the indeterminate form 00.
To solve limits of the form f(x)g(x), we use the property f(x)g(x)=eg(x)lnf(x).
Let L=limx→4π(cosx−sinx)(x−4π).
Then lnL=limx→4π(x−4π)ln(cosx−sinx).
For ln(cosx−sinx) to be defined in real numbers, the argument (cosx−sinx) must be positive.
cosx−sinx>0⟹cosx>sinx.
In the vicinity of x=4π, this condition holds for x<4π. Therefore, we must consider the left-hand limit, i.e., limx→(4π)−.
Let x=4π−h, where h→0+.
Then x−4π=−h.
And cosx−sinx=cos(4π−h)−sin(4π−h).
Using the compound angle formulas:
cos(4π−h)=cos4πcosh+sin4πsinh=21(cosh+sinh).
sin(4π−h)=sin4πcosh−cos4πsinh=21(cosh−sinh).
Substituting these into the expression for the base:
cosx−sinx=21(cosh+sinh)−21(cosh−sinh) =21(cosh+sinh−cosh+sinh) =21(2sinh)=2sinh.
Now, substitute these into the limit expression for lnL:
lnL=limh→0+(−h)ln(2sinh).
Using logarithm properties, ln(AB)=lnA+lnB:
lnL=limh→0+(−h)[ln2+ln(sinh)].
lnL=limh→0+[−hln2−hln(sinh)].
We evaluate each term separately:
-
limh→0+(−hln2)=0×ln2=0.
-
limh→0+(−hln(sinh)). This is of the form 0×(−∞) as h→0+ and sinh→0+, so ln(sinh)→−∞.
To apply L'Hopital's Rule, rewrite it as a fraction:
limh→0+1/h−ln(sinh). This is of the form ∞∞.
Apply L'Hopital's Rule:
limh→0+dhd(1/h)dhd(−ln(sinh))=limh→0+−h21−sinhcosh. =limh→0+sinhh2cosh.
This is of the form 00. We can rewrite it as:
limh→0+(sinhh⋅hcosh).
We know that limh→0+hsinh=1, so limh→0+sinhh=1.
Also, limh→0+hcosh=0×cos(0)=0×1=0.
Therefore, limh→0+(−hln(sinh))=1×0=0.
Combining the results for both terms:
lnL=0+0=0.
Since lnL=0, we have L=e0=1.
The final answer is 1.
Explanation of the solution:
- Identify the indeterminate form 00.
- Use logarithm: L=limx→af(x)g(x)⟹lnL=limx→ag(x)lnf(x).
- Analyze the domain of ln(cosx−sinx), which requires cosx−sinx>0. This implies taking the left-hand limit as x→4π.
- Substitute x=4π−h and simplify the expression.
- Evaluate limh→0+(−h)[ln2+ln(sinh)] term by term.
- The first term −hln2→0.
- The second term −hln(sinh) is of 0×(−∞) form, convert to ∞∞ form and apply L'Hopital's rule, or use standard limits like limh→0hsinh=1. This term also evaluates to 0.
- So, lnL=0, which means L=e0=1.
