Question
Question: $\lim_{x \to \frac{\pi}{2}} \left( \frac{\int_{x^3}^{(\pi/2)^3} (\sin(2t^{1/3}) + \cos(t^{1/3})) dt}...
limx→2π((x−2π)2∫x3(π/2)3(sin(2t1/3)+cos(t1/3))dt)
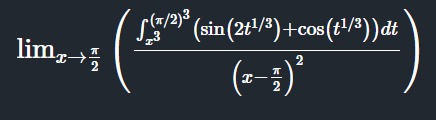
Answer
89π2
Explanation
Solution
The limit is of the indeterminate form 00. L'Hopital's Rule is applied twice. The derivative of the numerator is found using the Fundamental Theorem of Calculus and the chain rule. After the first application, the limit remains 00, necessitating a second application of L'Hopital's Rule. The derivatives of the resulting numerator and denominator are calculated, and evaluating them at x=2π yields the final answer.
