Question

$\lim_{x \to 7}\sqrt{(x-1)^{2015} \cdot (x-7)^{2026} \cdot (x-10)^{2027}}$

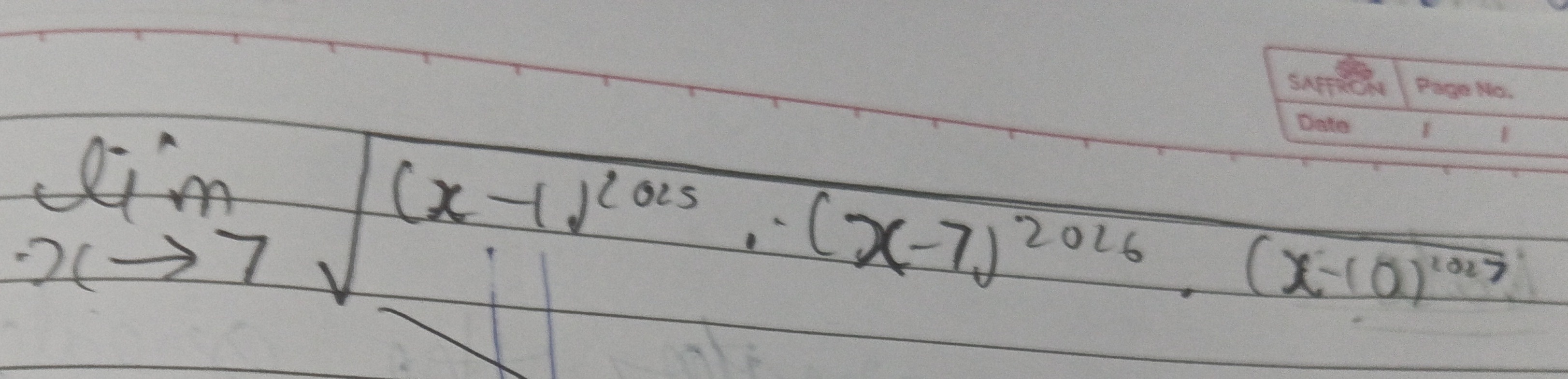
Answer 1

The limit does not exist

Answer 2

The function is $\sqrt{(x-1)^{2015} \cdot (x-7)^{2026} \cdot (x-10)^{2027}}$. For the function to be defined for real values, the expression inside the square root must be non-negative. Let $g(x) = (x-1)^{2015} \cdot (x-7)^{2026} \cdot (x-10)^{2027}$. Analyzing the sign of $g(x)$ near $x=7$, we find that for $x \in (1, 7) \cup (7, 10)$, $g(x) < 0$. This means the function is not defined as a real number in any punctured neighborhood of $x=7$. The domain of the function is $(-\infty, 1] \cup \{7\} \cup [10, \infty)$. Since $x=7$ is not a limit point of the domain, the limit as $x \to 7$ does not exist according to the standard definition of a limit.