Question
Question: $\lim_{x \to 3}\frac{\sqrt{3x-3}}{\sqrt{2x-4}-\sqrt{2}}$ is equal to...
limx→32x−4−23x−3 is equal to
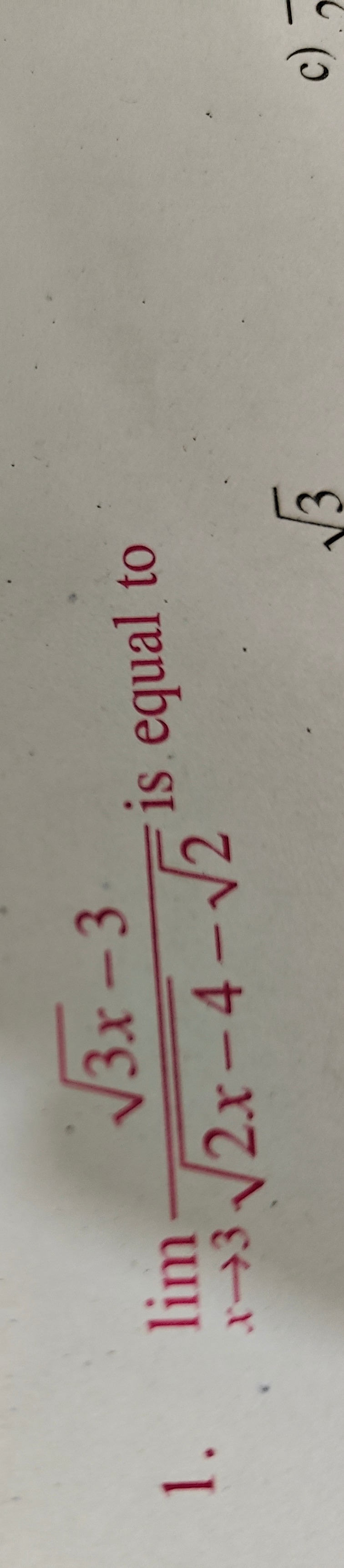
3
6
26
Does not exist
Does not exist
Solution
The given limit is limx→32x−4−23x−3.
Upon direct substitution of x=3: Numerator: 3(3)−3=9−3=6 Denominator: 2(3)−4−2=6−4−2=2−2=0
The form of the limit is 06. This indicates that the limit does not exist as a finite value. To determine the behavior, we analyze the one-sided limits:
Right-hand limit (x→3+): As x approaches 3 from the right (x>3), 2x−4 approaches 2 from values greater than 2. Thus, 2x−4 approaches 2 from values greater than 2. The denominator 2x−4−2 approaches 0 from the positive side (0+). The numerator approaches 6 (a positive value). So, limx→3+2x−4−23x−3=0+6=+∞.
Left-hand limit (x→3−): As x approaches 3 from the left (x<3), 2x−4 approaches 2 from values less than 2 (but greater than −4 for the square root to be defined). Thus, 2x−4 approaches 2 from values less than 2. The denominator 2x−4−2 approaches 0 from the negative side (0−). The numerator approaches 6 (a positive value). So, limx→3−2x−4−23x−3=0−6=−∞.
Since the left-hand limit (−∞) and the right-hand limit (+∞) are not equal, the limit limx→32x−4−23x−3 does not exist.
