Question

$\lim_{x \to 2024} \sqrt[V]{(x - 2023)^{2023}(x - 2024)^{2024} \cdot (x - 2025)^{2025}}$

Answer 1

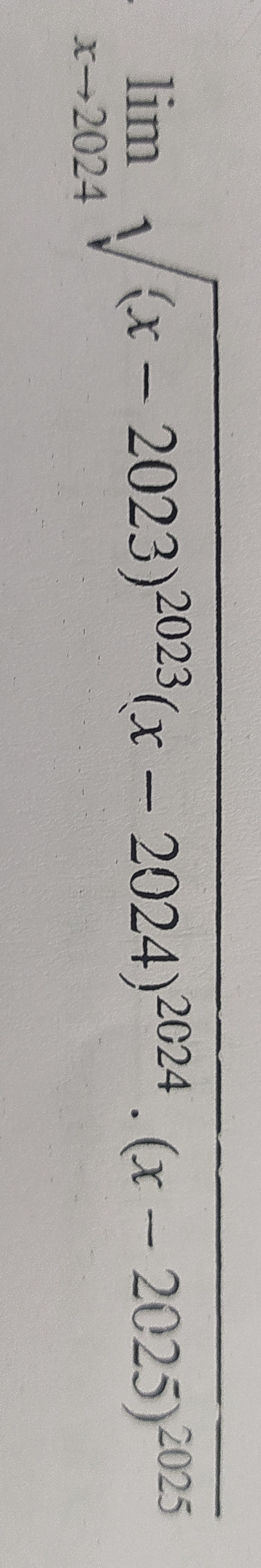
The limit does not exist

Answer 2

Let the given limit be $L$. The function is $f(x) = \sqrt[V]{(x - 2023)^{2023}(x - 2024)^{2024} \cdot (x - 2025)^{2025}}$. The notation $\sqrt[V]{\cdot}$ is unusual. Assuming it represents a root with index $V$. Based on the similar question which uses a square root, and the standard context of such problems in the specified exams, we assume $V=2$, i.e., it is a square root.

The function is $f(x) = \sqrt{(x - 2023)^{2023}(x - 2024)^{2024} \cdot (x - 2025)^{2025}}$. For the function to be defined for real values, the expression inside the square root must be non-negative. Let $g(x) = (x - 2023)^{2023}(x - 2024)^{2024} \cdot (x - 2025)^{2025}$. We need $g(x) \ge 0$.

We analyze the sign of $g(x)$ near the limit point $x=2024$. The roots of $g(x)$ are 2023, 2024, and 2025. Let's consider the sign of $g(x)$ in a punctured neighborhood of 2024, i.e., for $x$ close to 2024 but $x \neq 2024$.

For $x$ slightly less than 2024 (e.g., $x = 2024 - \delta$ for a small $\delta > 0$):

• $(x - 2023)^{2023}$: $x - 2023 = 1 - \delta > 0$. Since the exponent 2023 is odd, $(x - 2023)^{2023} > 0$.
• $(x - 2024)^{2024}$: $x - 2024 = -\delta < 0$. Since the exponent 2024 is even, $(x - 2024)^{2024} > 0$ for $x \neq 2024$.
• $(x - 2025)^{2025}$: $x - 2025 = -1 - \delta < 0$. Since the exponent 2025 is odd, $(x - 2025)^{2025} < 0$.

So, for $x$ slightly less than 2024, $g(x) = (\text{positive}) \cdot (\text{positive}) \cdot (\text{negative}) = \text{negative}$.

For $x$ slightly greater than 2024 (e.g., $x = 2024 + \delta$ for a small $\delta > 0$):

• $(x - 2023)^{2023}$: $x - 2023 = 1 + \delta > 0$. Since the exponent 2023 is odd, $(x - 2023)^{2023} > 0$.
• $(x - 2024)^{2024}$: $x - 2024 = \delta > 0$. Since the exponent 2024 is even, $(x - 2024)^{2024} > 0$ for $x \neq 2024$.
• $(x - 2025)^{2025}$: $x - 2025 = -1 + \delta$. If $\delta$ is small enough (e.g., $\delta < 1$), $x - 2025 < 0$. Since the exponent 2025 is odd, $(x - 2025)^{2025} < 0$.

So, for $x$ slightly greater than 2024, $g(x) = (\text{positive}) \cdot (\text{positive}) \cdot (\text{negative}) = \text{negative}$.

Thus, in any punctured neighborhood of $x=2024$, the expression inside the square root, $g(x)$, is negative. The function $f(x) = \sqrt{g(x)}$ is not defined for real values in any punctured neighborhood of $x=2024$. For a limit $\lim_{x \to c} f(x)$ to exist, the function $f(x)$ must be defined in some punctured neighborhood of $c$. Since this condition is not met for $c=2024$, the limit does not exist in the real number system.

The domain of $f(x)$ where $g(x) \ge 0$ is $(-\infty, 2023] \cup \{2024\} \cup [2025, \infty)$. The point $x=2024$ is an isolated point in the domain. The limit $x \to 2024$ requires considering values of $x$ arbitrarily close to 2024 but not equal to 2024. Since there are no domain points in any punctured neighborhood around 2024, the limit does not exist.

If $V$ were an odd integer, the root would be defined for negative numbers as well, and the function would be defined for all real $x$. In that case, the limit would be $\sqrt[V]{(1)^{2023} \cdot (0)^{2024} \cdot (-1)^{2025}} = \sqrt[V]{0} = 0$. However, given the similar question, the even root case (specifically square root) is the intended interpretation.